Walking Under Ladders-- I
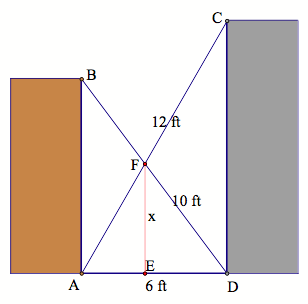 A 6-foot wide alley has both walls perpendicular to the ground.
A 6-foot wide alley has both walls perpendicular to the ground.
Two ladders, one 10 feet long, the other 12 feet, are propped up from opposite bottom corners to the adjacent wall, forming an X shape.
All four legs of each ladder are firmly touching either the bottom corner or the opposite wall.
The two ladders are side by side and also touching each other at the intersection of the X shape.
What is the distance (in Feet) from the point of intersection to the ground?
The answer is 4.52.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
This is the way I did it, but I really hope there's a better way than analytic geometry. :P
△ A F E and △ A C D are similar, so are △ D F E and △ D B A . Let A E = a , then:
x a = C D A D = 3 1 ( ∠ A C D = 3 0 o )
Similarly.
x 6 − a = B A A D = 4 3 ( △ D B A = 3-4-5 △ )
Adding the two equations together:
⇒ x 6 = 3 1 + 4 3
⇒ x = 3 1 + 4 3 6 = 4 . 5 2
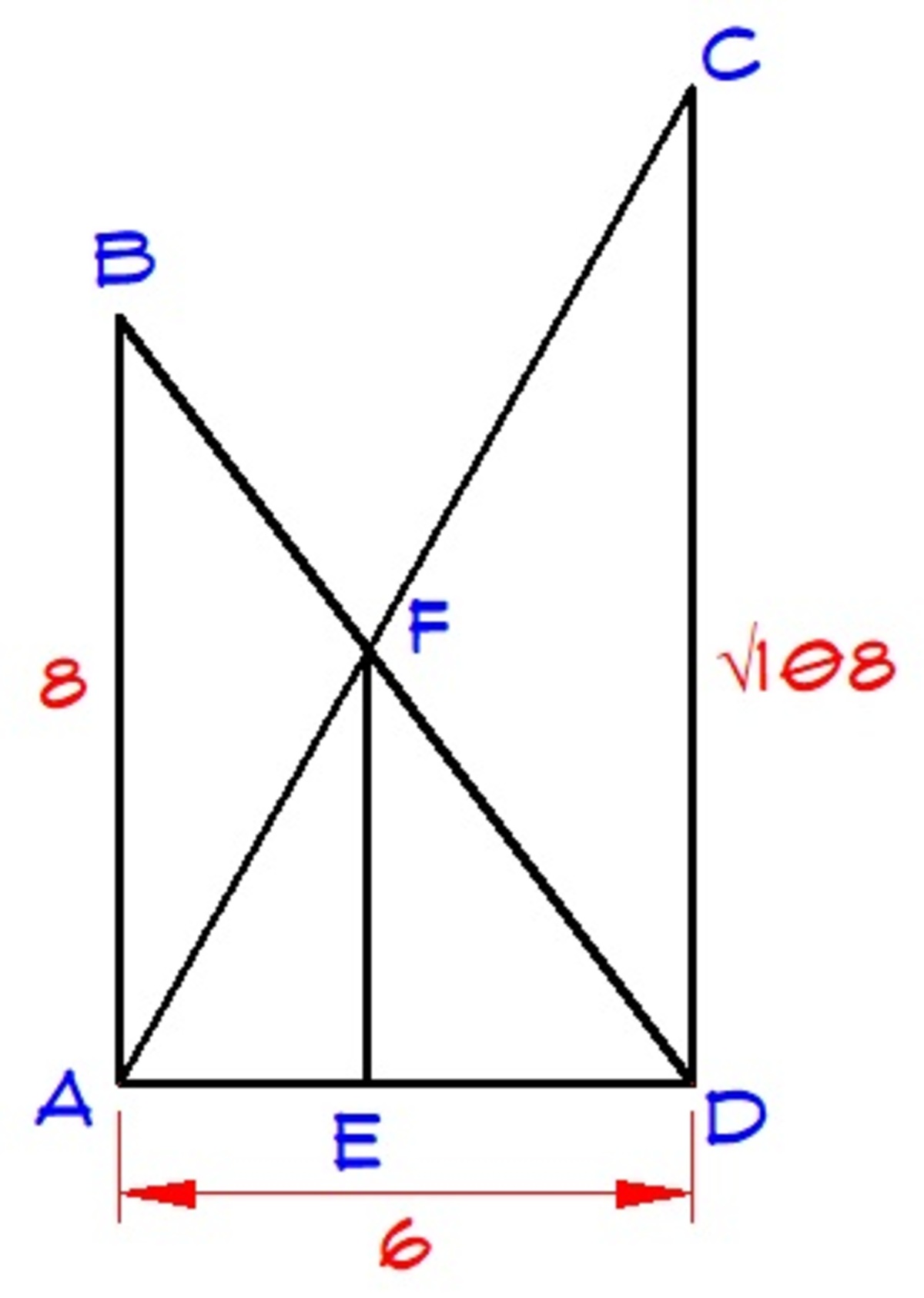 By pythagorean theorem, we have
By pythagorean theorem, we have
C D = 1 2 2 − 6 2 = 1 0 8
A B = 1 0 2 − 6 2 = 6 4 = 8
Since △ F E A ∼ △ C D A , F E A E = C D A D = 1 0 8 6
Since △ F E D ∼ △ B A D , F E E D = A B A D = 8 6 = 4 3
Now we add
F E A E + F E E D = 1 0 8 6 + 4 3
But A E + E D = A D = 6 , so
F E A D = 1 0 8 6 + 4 3
F E 6 = 1 0 8 6 + 4 3
F E ≈ 4 . 5 2
Note:
We can use the formula x 1 = a 1 + b 1 . Now substitute,
x 1 = 8 1 + 1 0 8 1
x ≈ 4 . 5 2
Let point A be the origin and line segment A D lie along the positive x -axis.
Now by Pythagoras A B = 8 ft. and C D = 6 3 ft.. So D B lies on the line y = − 3 4 x + 8 , and A C lies along the line y = 3 x . These two lines intersect when
− 3 4 x + 8 = 3 x ⟹ 8 = x ( 3 4 + 3 ) ⟹ x = 4 + 3 3 2 4 ft..
This gives us the height of the point of intersection as
y = 3 ∗ 4 + 3 3 2 4 = 9 + 4 3 7 2 = 4 . 5 2 ft. to 2 decimal places.