Walking Under Ladders -- II
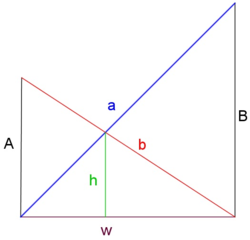 An alley has both walls perpendicular to the ground.
An alley has both walls perpendicular to the ground.
Two ladders, one 3 feet long, the other 2 feet, are propped up from opposite bottom corners to the adjacent wall, forming an X shape.
All four legs of each ladder are firmly touching either the bottom corner or the opposite wall.
The two ladders are side by side and also touching each other at the intersection of the X shape.
The distance from the point of intersection to the ground (h)is 1 foot.
What is the width, w of the alley (in feet)? Given your answer to 2 decimal places.
The problem is not original.
The answer is 1.23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let width w of alley = x+y where the horizontal h meets ground
Now B^2 +w^2 = 9 and A^2 +w^2 = 4
B^2 - A^2 = 5 ----------------------------(1)
By similar triangles,
A/w= h/y so y= w/A since h=1--------(2)
B/w = h/x so x = w/B since h = 1-------(3)
x+y = w
So w/A+w/B = w -----------------------------from (2), (3)
1/A+1/B= 1
A+B= AB
B= A/(A-1)---------------------------------(4)
Putting (4) into (1)
(A/A-1)^2 - A^2 = 5
A^4-2A^3+5A^2-10A +5 = 0
Solving quartic, A = 1.576
width w = 1.231
Nice problem and solution. But that looks ugly.Please LATEX-ify it.
Draw a line parallel to the base through the point where the ladders intersect. Divide the base into x and W - x, where x is to the left of the vertical line to the intersection and W - x is to the right . By similar triangles, x/(W - x) = 1/(B - 1), so B = W/x. Also, by similar triangles, x/(W - x) = (A - 1)/1, so A =W/(W - x). Now, A^2 + W^2 = 4 and B^2 + W^2 = 9, so B^2 - A^2 = 5. Substituting for A and B, W^2/x^2 - W^2/(W - x)^2 = 5, or W^4 - 2W^3 x =5x^4 - 10W x^3 + 5x^2 W^2. Transposing and letting x = rW, 5 r^4 W^4 - 10 r^3 W^4 +5 r^2 W^4 +2 r*W^4 - W^4 = 0. Dividing by W^4, 5r^4 -10r^3 +5r^2 + 2r - 1 =0. = 1/r = Solving by Newton-Raphson with an initial guess of r_0 = 0.4, r= .36553405. Then B = W/x = 1/r = 2.735723252. Then W^2 = 9 - B^2 = 1.515818288, and W = 1.231185724.
F o r t h e t w o l a d d e r p r o b l e m , A 1 + B 1 = h 1 = 1 . ⟹ B = A − 1 A . . . . . . . . . . . . ( 1 ) A g a i n s o l v i n g r i g h t ∠ e d Δ s , W 2 = a 2 − B 2 = b 2 − A 2 . S u b s t i t u t i n g ( 1 ) i n t h i s w e g e t a q u a r t i c i n A , A 4 − 2 A 3 + ( 1 − A ) 2 ( a 2 − b 2 ) = 0 . S o l v i n g A = 2 . 7 3 5 7 . ∴ W = b 2 − A 2 = . 2 3 1 2 2 2 .
Let the two parts of the width be c and w − c from left to right. By similar triangles we get:
w − c = A w c = B w
Adding them we get 1 = A 1 + B 1 .
Now, by the Pythagorean Theorem we know that:
A 2 + w 2 = 4 ⟹ A = 4 − w 2 B 2 + w 2 = 9 ⟹ B = 9 − w 2 .
Substituting them into the first equation we get:
1 = 4 − w 2 1 + 9 − w 2 1
After simplifying we get:
w 8 − 2 2 w 6 + 1 6 3 w 4 − 4 5 4 w 2 + 3 8 5 = 0
That is a bi-quartic equation in w 2 . Using Newton Raphson method we get w ≈ 1 . 2 3 1 1 .
Nice problem, you should also try this problem .