War time
A war is going on between two countries. The situation is as shown in the image below.
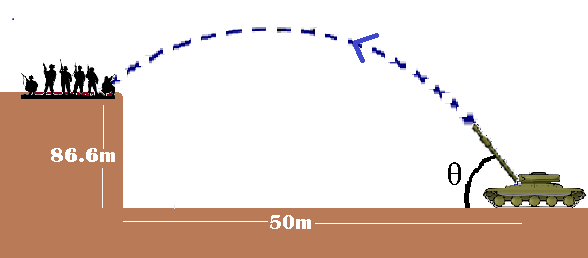
The image is not correct to the measurements given.
A tank has to fire a target which is at horizontal distance 50m and at a height 86.6m as shown in the image. is the angle made by the cannon with the ground as shown in the image.The cannon shoots in trajectory motion. The speed with which the cannon ball is shot, directly depends on the power used by the cannon. Air resistance is negligible.
(Cannon the gun part of a tank ; Cannon ball projectile).
What is the approximate value of so that the cannon uses minimum power?
This is an original problem and belongs to my set Raju Bhai's creations
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Given, power is directly proportional to initial velocity,
If power is minimum, initial speed must be minimum.
Construct a line from the tank to the target. Let the angle made by the line with ground be α
t a n α = 5 0 8 6 . 6 ⟹ α = 6 0 °
Let the angle between the line and projection be β .
This arrangement looks like projectile in an inclined plane .
Range in an inclined plane is given by-
R = g c o s 2 α u 2 2 c o s β s i n ( α + β )
u 2 = 2 c o s β s i n ( α + β ) R g c o s 2 α
Since R,g, α are constant. u to be minimum , c o s β s i n ( α + β ) must be maximum.
To find maximum value, differentiate it and equate it to 0.
We get α + β = 4 5 ° + 2 α
According to diagram, α + β = θ , α = 6 0 °
Therefore, θ = 7 5 °