Warm up problem 16: area of quad easy-medium
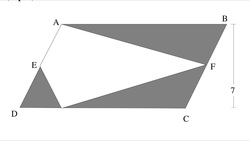 If
C
D
=
1
2
and E and F are the mid points of
A
D
and
B
C
respectively, find the area of the shaded area.
If
C
D
=
1
2
and E and F are the mid points of
A
D
and
B
C
respectively, find the area of the shaded area.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
As their is no details about a point in diagram thus the area will not change if we change the location of tha point . So I have moved this poin to D . Thus figure is divided into 3 triangles . And further I used the property that AREA OF TWO TRIANGLE IS SAME IF THEY HAVE COMMON BASE AND ARE BETWEEN TWO PARALLEL LINES. thus I have moved the point F to point C and thus the required area is half of the area of the parallelogram i.e. 42 . :)
-
Join E and F. DC = EF = AB = 12. Let points E and F meet DC at X. Given DC = base = 12. Also given, height of the parallelogram = perpendicular height = 7.
-
Since E and F are the mid-points of AD and BC, the perpendicular distance to AB and DC are the same. This is same as the perpendicular distance from X to EF. That means, perpendicular distance from X to EF and perpendicular distance from F to AB are one and the same. Also EF = AB.
-
Thus, area of triangle EFX = area of triangle ABF.
-
Hence, area of the shaded region = half the area of the whole parallelogram = (1/2)xbasexheight = (1/2)x12x7 = 42.
OR
Let's take the shaded regions itself.
-
Area of shaded region = Area of triangle EDX + area of triangle FXC + area of triangle ABF.
-
The altitudes for triangles EDX and FXC are one and the same. Thus, the sum of their areas = 1/2 * DX * h + 1/2 * XC * h = 1/2* h * (DX+XC) = 1/2 * h * DC = 1/2 * 3.5* 12 = 21.
-
Area of triangle ABF = 1/2 * 12 * 3.5 = 21.
-
Finally, the area of the shaded region = 21+21 = 42.
In the picture, B C = 7 cm , and F is a mid point of B C , and we know that △ A B F = △ E G F , where the point G is a point on C D . Then, the shaded area is equal to □ E D C F , so we get □ E D C F = 1 2 × 3 . 5 = 6 × 7 = 4 2 .
Note: the reason that △ A B F = △ E G F is if we draw a line E F , then □ A E F B = □ E D C F because F and E are a mid point. Then, we draw a line A F and E C , then we get △ A B F = △ A E F = △ E F C = △ E D C .
Hence, the area of shaded area is 4 2 cm 2 .
Triangle AFB is congruent with/to Triangle AFE, which in turn is congruent to EMF [ M being the vertex point on DC ]. Congruent triangles have equal areas. So required area = ar(EDM) + ar(EMf) + ar(FMC) = ar(EDCF) = 1/2 * ar(ABCD) = 1/2 * DC * 7 = 42 [ area of a parallelogram = base * altitude ]
Join E and F Then the area of the white portion can be took out by 3.5x12 The area of the quadrilateral ABCD is 12x7 Area of shaded portion is 12x7 - 3.5x12 = 42
Lemma: if two opposite mid points are connected on a parallelogram, then, regardless of the other two points' position on the other two sides, the area of the quadrilateral created will be 1/2.
Proof:
Because the new triangle will be made of two triangles with the same base and 1/2 the height of the reference quadrilateral, we can express the area of the original quad as b h and the new one as 2 ( 2 2 h ∗ b ) ⇒ 2 b h