Deduce the Sum of the Exponents
2 x = 2 y 1 , x + y = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Could it be 2^x=2^-y So x=-y And x+y=0
That is what I did
2^x=2^-y
so x is negative and y is positive
and -x = y
then x + y = 0
I did it that way too
Anything to the negative power is going to be positive when it is made in its reciprocal form. Since here we have 2^x, keep "x" as -1. Then y=1. So we get x + y = -1 + 1 = 0
I also used the logarithm... 2 x 2 x lo g 2 2 x x ⋅ lo g 2 2 x ⋅ 1 x + y = 2 y 1 = 1 ⋅ 2 − y = lo g 2 2 − y = − y ⋅ lo g 2 2 = − y ⋅ 1 = 0
2 x = 2 y 1 = 2 − y ⟹ x = − y ⟹ x − ( − y ) = 0 ⟹ x + y = 0
- 2 x = 2 y 1
- 2 x ⋅ 2 y = 1
- 2 x + y = 2 0
- x + y = 0
Exponent laws key
Isolate for 1, and solve
Product of powers give zero.
From the equation, we know that 2^x = 2^-y. So, it means x = -y. Then, x+y = 0
to have 2^x=1/2^y, you would have to have x be negative so when you inverse , it becomes positive. That means that x=-y, o the answer is 0
2^x=1/2^y=2^-y =)x= -y =)x+y=0
2^(-1) = 1/2^(1) :. (-1) + 1 = 0
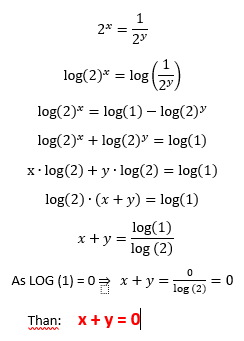
1 = 2 0
2 x ( 2 x ) ( 2 y ) 2 x + y 2 x + y ∴ x + y = = = = = 2 y 1 1 1 2 0 0