Warped Gravity
In an imaginary Universe, The force of gravity does not follow the Newtonian inverse square law but rather is proportional to the square of the distance between two masses.
F 2 1 ∝ M 1 M 2 ( r 2 − r 1 ) 2
The proportionality constant is G = 2 . 2 8 8 7 1 6 5 6 2 × 1 0 6 N / m 2 ⋅ K g 2
All other physical laws are identical
In such a universe, two similar positively charged and isolated rods A and B are suspended in air, exactly above one another, and kept vertically apart a distance Δ such that, for small displacements, the rod B oscillates up and down (not necessarily simple harmonically) about the imaginary line O O ′
Rod A is kept fixed.
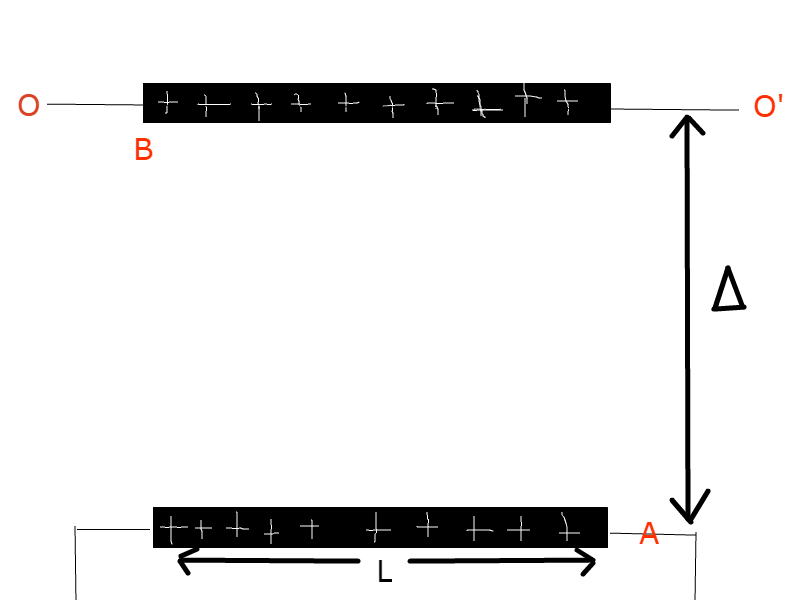
Find distance Δ if, L i n e a r M a s s D e n s i t y ( β ) = 2 K g / m L i n e a r C h a r g e D e n s i t y ( λ ) = 3 C / m L e n g t h o f r o d s ( L ) = 2 4 m 4 π ε 0 1 = 9 × 1 0 9 N ⋅ m 2 / C 2
Give your answer as a number with 2 places after the decimal point
The answer is 7.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Yeah actually what happened was i took the distance to be 7 meters and then solved for G instead, which is why i gave it to such precision! To ensure that the answer indeed came out to be 7!
Log in to reply
I thought you probably did. The problem would have looked better, however, if you had solved for G using a more accurate value of 4 π ε 0 1 than the one you used.
Log in to reply
Yeah thankyou! I will make sure to take that into account the next time!
The repulsive force between the two rods is perpendicular to the rods, and of magnitude F 1 = 4 π ε 0 λ 2 ∫ 0 L ∫ 0 L Δ 2 + ( x − y ) 2 d x d y × Δ 2 + ( x − y ) 2 Δ = 4 π ε 0 λ 2 D ∫ 0 1 ∫ 0 1 ( D 2 + ( X − Y ) 2 ) 2 3 d X d Y where Δ = D L , using the substitution x = L X , y = L Y . With the double substitution U = X + Y , V + X − Y , we have ∫ 0 1 ∫ 0 1 ( D 2 + ( X − Y ) 2 ) 2 3 d X d Y = 2 1 ∫ − 1 1 d V ∫ ∣ V ∣ 2 − ∣ V ∣ ( D 2 + V 2 ) 2 3 d U = ∫ − 1 1 ( D 2 + V 2 ) 2 3 1 − ∣ V ∣ d V = 2 ∫ 0 1 ( D 2 + V 2 ) 2 3 1 − V = D 2 2 ( D 2 + 1 − D ) where the last integral is performed by standard tricks, and so F 1 = 4 π ε 0 2 λ 2 D D 2 + 1 − D Smiilarly, the attractive gravitational force between the rods, and of magnitude F 2 = G β 2 ∫ 0 L ∫ 0 L ( Δ 2 + ( x − y ) 2 ) Δ 2 + ( x − y ) 2 Δ d x d y = G β 2 L 4 D ∫ 0 1 ∫ 0 1 D 2 + ( X − Y ) 2 d X d Y and the same substitution and similar standard integration tricks give F 2 = 3 1 G β 2 L 4 D { D 2 + 1 + 2 D 3 − 2 D 2 D 2 + 1 + 3 D 2 ln ( D D 2 + 1 + 1 ) } We want to find the equilibrium position, namely the value of D for which F 1 = F 2 . This simplifies down to the equation 4 π ε 0 G β 2 L 4 6 λ 2 = D 2 [ 1 − D 2 + D D 2 + 1 + 3 D 2 ( D 2 + 1 + D ) ln ( D D 2 + 1 + 1 ) ] With the given values of the parameters, we can solve this equation numerically to obtain D = 0 . 2 9 1 6 6 6 6 6 6 6 7 , and hence Δ = 7 .
It is a little weird that G is given to such precision, and yet 4 π ε 0 1 is given to just one significant figure!