Wasn't it easy to find an equilateral triangle's side

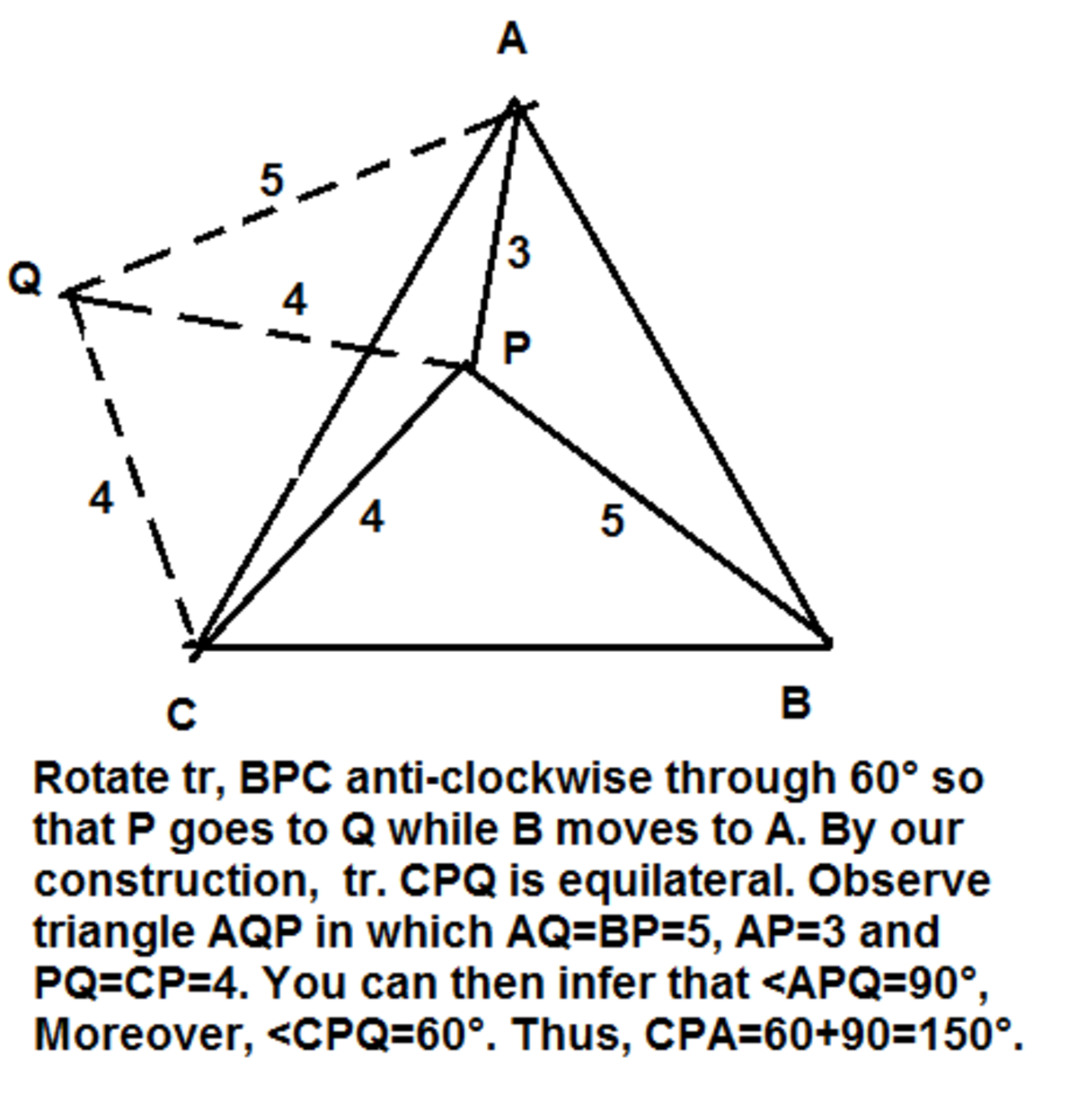
Draw a point $Q$ so that triangle $ACQ$ has side lengths $CQ = 4, AQ = 5$ and $AC = a$ being the side of the given equilateral triangle $ABC$ . This makes triangle $ACQ$ congruent to triangle $BCP$ .

Then, since $CP = CQ = 4$ , triangle $PCQ$ is isosceles. Also, since $\angle BCA = 60$ degrees and triangles $ACQ$ and $BCP$ are congruent, we have that $\angle PCQ = 60$ degrees as well. This fact, together with the facts that $CP = CQ = 4$ , implies that triangle $PCQ$ is in fact equilateral, and thus $PQ = 4$ . But with $PQ = 4, AP = 3$ and $AQ = 5$ we have that triangle $APQ$ is a right angled triangle with $\angle APQ = 90$ degrees.

Thus $\angle APC = 60 + 90 = 150$ degrees. Now we just need to use the Cosine Law on triangle $APC$ to find that

$(AC)^{2} = (AP)^{2} + (PC)^{2} - 2(AP)(PC)\cos(\angle APC)$

$\Longrightarrow a^{2} = 3^{2} + 4^{2} - 2(3)(4)\cos(150)$

$\Longrightarrow a^{2} = 25 + 12\sqrt{3} \Longrightarrow a = \sqrt{25 + 12\sqrt{3}} = \boxed{6.766}$ to $3$ decimal places.

Rotate about C by angle 60 and use cosine formula

@Julien Bongars

Using an identity $2\Delta xxx=\Delta aaa+\Delta bbb+\Delta ccc+3\Delta abc$ we can easily get a formula for any three numbers. This is closely related to the formula of the Napoleon triangle side. The triangle side as explained in this problem is in fact $\sqrt {3} x$ where x is the length of the Napoleon equilateral triangle. The formula is: $\sqrt{(4 \sqrt{3} A + a^2 + b^2 + c^2)/2}$ where A is area of a triangle formed from $a, b, c$ .

These kind of problems can be solved for any values of distances of point P from the three vertices. I have a generalisation for this using rotation and then evaluating the areas of the rotated figures.