Wasn't it easy to find an equilateral triangle's side
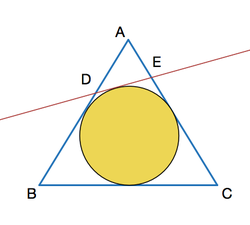A
B
C
is an equilateral triangle.
D
E
is the tangent to the inscribed circle with
D
on
A
B
and
E
on
A
C
. It is given that
D
E
perpendicular to
A
C
and
A
E
=
1
0
.The side length of
A
B
C
can be expressed as
a
+
b
c
where
a
and
b
are positive integers and
c
is square-free positive integer; then find
a
+
b
+
c
.
The answer is 43.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Great solution. In this problem many people forget the quadrilateral B D E C and focus on other non-required parts.
And i dont understand the process of AX + AY
Log in to reply
Since X and Y are mid-points of AB and AC respectively,
AB=AX+XB=2AX=AX+AY
I have a doubt regarding this...I consider the given circle as the incircle and draw the angle bisector of angle A meeting DE at say K. Now in triangle AKE, angle AEK = 90 and as AK is angular bisector so angle KAE = 30 which gives AK = 20/(under root 3). let AK meets BC at M so AM = AK + KM = [20/(under root 3)] + 2r where r is the inradius Also as ABC is equilateral traingle , inradius r = side/(2*root 3) and angle bisector is same as altitude in equilateral traingle so AM also equals (root 3 * side /2) equating the two values of AM gives side = 40.. can you guide me where I am wrong?
Log in to reply
A M = A K + 2 r because AK does not meet the circle.
Log in to reply
I guess I got your point...it is not necessary that AM has to touch circle at the point where DE is tangent to it...is it what you are saying...right?
how is DX +EY=DZ+EZ?
Now that is see it I regret i didnt even thought of using trigonometry
Could you please post a picture of your way of thinking? my english is bad so i dont understand where u put the x y and z
Log in to reply
X is where the circle touches AB.
Y is where the circle touches AC.
Z is where the circle touches DE.
How do you know that ADE is a 30,60,90 triangle? Do all equilateral triangles have three 60 degrees?
Log in to reply
nevermind, just wikipedia'd the definition of that type of triangle.
The incenter’s center can be found from the intersection of the angle bisectors of the triangle. Given that the triangle is equilateral, a 30-60-90 triangle is formed from the vertex, the point of tangency from AC, and the center. Letting x be the radius of the circle, 3 1 0 + x = x , solving for x , x = 5 + 5 3 . Since the given triangle is equilateral, the point of tangencies are the midpoints of the sides. So side = 2 ( 5 + 5 3 + 1 0 ) = 2 ( 1 5 + 5 3 ) = 3 0 + 1 0 3 . a + b + c = 3 0 + 1 0 + 3 = 4 3
I L A T E X 'ed everything. Click the edit button to see the code.
You should use L a t e x .
I did it exactly the same way :D
Denote the incircle center Z , X the point of tangency of ( D E ) on the circle and I the middle of [ A Z ] . One can check that Z X E I is a square, which side is the radius ( = : r ) of the incircle. Therefore, considering the symmetry, the side length ( = : l ) is : l = 2 0 + 2 r .
The problem is resumed to finding the radius of the inner circle of an equilateral triangle. Since the bisectors are also the medians, r is also the centroid, and therefore equal to ont third of the altitude : r = 2 3 l . Hence, l = 2 0 + 2 × 2 3 l = 3 0 + 1 0 3
Denote the incircle's tangency on A B , A C , D E as X , Y , Z . Since A D E is a 3 0 , 6 0 , 9 0 triangle, we have A D = 2 0 , D E = 1 0 3 . Since A B C is equilateral, X , Y are midpoints of A B , A C , hence its side length is equal to A X + A Y = A D + A E + D X + E Y = 3 0 + D Z + E Z = 3 0 + D E = 3 0 + 1 0 3 and our answer is 1 0 + 3 0 + 3 = 4 3 .