Water Bottle
 A large glass bottle when filled with water has a mass of 15kg.
A large glass bottle when filled with water has a mass of 15kg.
When this bottle is half filled with water, it has a mass of 10kg.
What is the mass of this glass bottle in kg?
Image Credit: Flickr Ashley .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
This question can also be looked at logically. If we empty half of the bottle, we lose 5kg. This means that half the mass of water is 5kg, and the mass of the water is 10kg. Hence the mass of the bottle from either of the statements is 5kg.
Thanks for your solution
Thank you!
B = m a s s o f b o t t l e
W = m a s s o f w a t e r
B + W = 1 5 ⟹ W = 1 5 − B ( 1 )
B + 2 1 W = 1 0 ( 2 )
Substitute ( 1 ) in ( 2 )
B + 2 1 ( 1 5 − B ) = 1 0 ⟹ B + 2 1 5 − 2 B = 1 0 ⟹ 2 1 B = 1 0 − 2 1 5 ⟹ B = 5
x means bottle weight,y means water weight. x+y=15.....(1) x+1/2 (y)=10......(2) from( 2), 2x+y=20......(3) then, (3)-(1) x=5
5kg.. wth, how huge this glass bottle.. how can you brought such of this thing? anyway this is a barrel not a bottle.. or maybe a bottle with lid made from a barble
Let x represent the mass of the bottle (in kg). Let y represent the mass of the water (in kg).
- x+y = 15
- x+0.5y = 10
Using the method of elimination... x+y = 15 (subtraction) x+0.5y = 10
0.5y = 5
Since 0.5y = 5, multiplying both sides by 2 shows that y = 10
Now we substitute this value into the first equation: x+(10) = 15 x = 5
Therefore, the mass of the bottle is 5 kg.
let total weight of glass be x kg
(15-x)= 2(10-x) 15-x = 20-2x x=5
It is a simple system of equations / matrix: It can be solved by hand, a calculator, or a program in C.
| 1 1 15 |
| .5 1 10 |
The first column represents weight of the water while the second column represenrs the weight of the glass. :)
Simple ..mass of bottle with fully filled water is 15kg and half filled is 10 kg so the difference is 5kg ..the mass of bottle is same so the difference 5 kg is mass of water increase that is the mass of water that occupies the remaining half and is equal to the present half ..from the given problen the mass of half filled bottle is 10kg so when we substitute mass of water we get mass of bottle is 5kg.
mass(B)+mass(w)=15................(1) mass(B)+0.5*mass(w)=10..........(2)
if we do equation (1) - equation (2) >>> then we will find>> mass (w)=10 putting this value of mass(w) in equation(1) or equation (2)>>>> then we can find >>> mass(B)=5
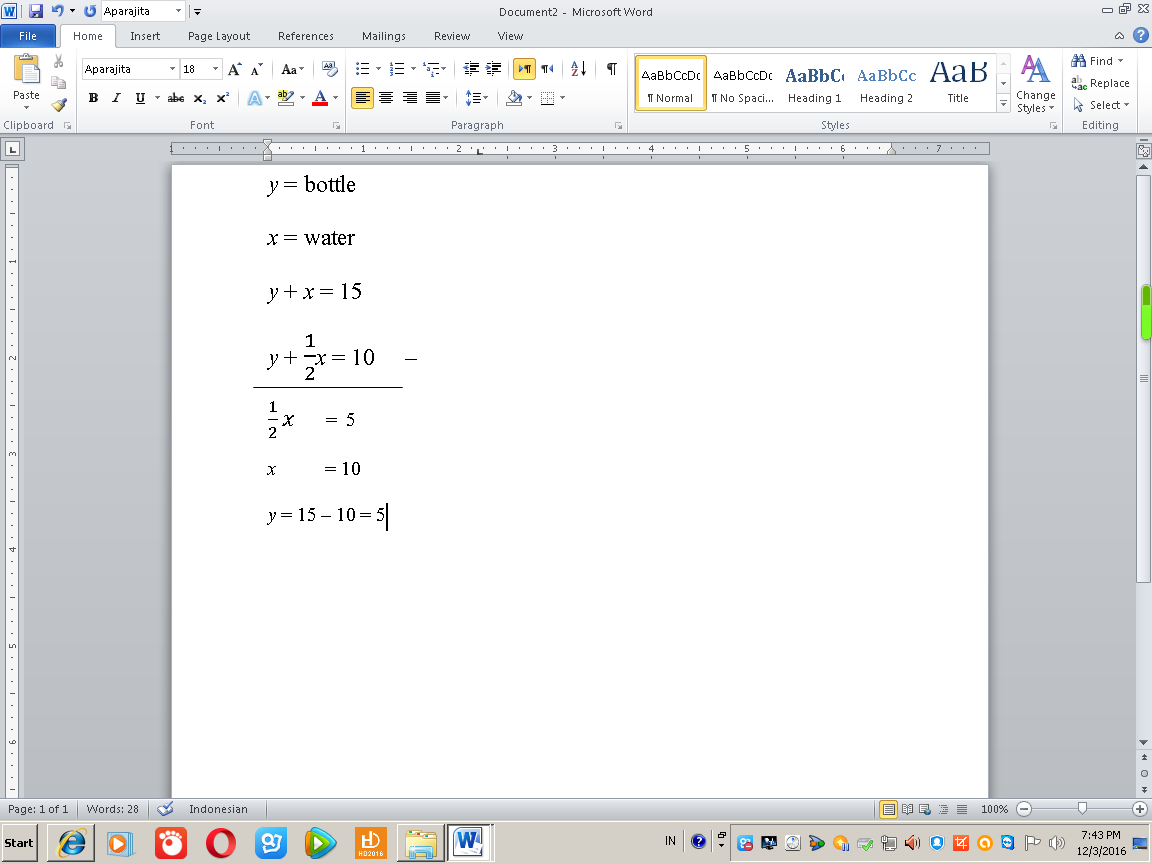
Let weight of bottle be x and weight of half the amount of water in bottle initially be y.
x+2y=15
x+y=10 or 2x+2y=20
subtracting first equation from second, we get x=5.