Water Bucket out of the world !
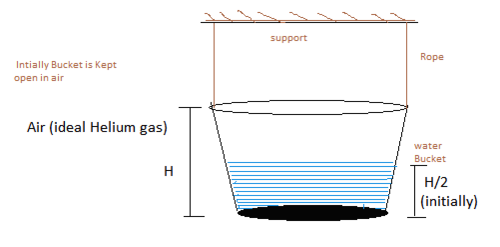 Consider an water Bucket (known as " Balti " in Indian language ) which is half filled. It has a shape of an frustum (refer to figure). It has upper radius 'b' and lower radius 'a' and Hight H. It is hanging on a fixed support and initially kept open in atmosphere ( in presence of air having Heat capacity ' C ' ).
Consider an water Bucket (known as " Balti " in Indian language ) which is half filled. It has a shape of an frustum (refer to figure). It has upper radius 'b' and lower radius 'a' and Hight H. It is hanging on a fixed support and initially kept open in atmosphere ( in presence of air having Heat capacity ' C ' ).

Now this bucket is tightly Packed at the top at time t=0 , and instantly (at t=0) a small hole of cross sectional area A h o l e is made at the centre of the base of this hanging bucket , so that water is starts coming out. Then Find the Time Interval ( T ) in which water level fall's half of it's initial hight . (Means Final Hight Becomes H/4 from bottom. )
Report Answer as : ⌊ T ⌋
Here : ⌊ . ⌋ i s G I F
Assumptions
∙ Assume that whole atmosphere is made of Ideal Helium gas (Mono atomic)
∙ In whole Event, this Ideal Gas has constant Heat capacity C = 2 R J/mole/k where 'R' is universal gas constant.
∙ Neglect Heat capacity and thermal expansion of Liquid and Bucket . Neglect Viscosity , surface Tension.
∙ You may Use wolfram alpha for calculation .
Details
a = 1 m , b = 2 m , H = 1 m , A h o l e = 0 . 0 1 m 2 , ρ w = 1 0 3 k g / m 3 , P a t m = 1 0 5 N / m , g = 1 0 m / s 2
This is Original .
Try More Deepanshu's Mixing of concept's .
The answer is 26.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Well This Time I'am Able to solve this Question , Since I Already Know concept of this question from Your Previous Post . But Yes I don't deserve these Point's . Since I could Not make conclusion at my own. it was really Tough .
Same way! the rather interesting thing however is that the expression becomes undefined when h= (1/10^4 pi^2)^(1/4)-1 , which means that at that height, the pressure outside is just enough or more to support the weight of water above the hole and the weight or pressure force of the helium above it, which is pretty awesome,
It would have been much simpler if baltis were cylinders
Log in to reply
huh , I Don't unnecessarily take It as " Balti " instead of cylinder , Indeed This Question is Little Based On My Real Life Incident , which Happen's before 4-5 days ago . Actually In that morning my mother ask me for bring a balti the from our Backyard , There are 3-4 balti 's and I pick wrong one , which has small hole in bottom , I didn't Know about that , so our water is leaked from it and our freshly washed house get again wet , and Beacuse of such carlessness my mom highly scolded me , so after that I just got inspiration to just created this situation .
And You Tell me what is shape of genral ' balti ' ? Affcourse this is reason why I take it as frustum shape. So Please Don't say Like this !
Log in to reply
Great source of inspiration :)
I am really sorry, i didnt mean in an offensive fashion, i just said that it would have been simpler in an ideal case, let me rephrase it
I fully acknowledge that this is the realistic case and definitely thats the problem i must solve if i am ever to understand water leak from a closed balti :)
Yes it only complicates the integral we have to put into wolfram alpha.
How is the process polyprotic with P/V =k
Log in to reply
use the given fact that specific heat capacity of process is 2R,
so dQ/dT = 2R now use dU+dW=dQ
and finally use PdV = dW and PV=nRT, you will get it
Yes As saketh said , But There is an standard relation for Heat capacity for Polytropic process : C = C v + 1 − x R ⇒ x = − 1
At any intermediate x .
Firstly radius of the junction of water and air can be given as :
r = a + H ( b − a ) x
Thanks to your values it comes out a neat :
r = 1 + x
Secondly height of air column = 1 − x
Hence volume of air column(by using the formula for volume of frustum) as :
V a i r = 3 π ( 1 − x ) ( ( 1 + x ) 2 + 2 2 + 2 ( 1 + x ) )
⇒ V a i r = 3 π ( 1 − x ) ( x 2 + 4 x + 7 )
Also volume of air initially (i.e x = 2 1 )
V i = 2 4 3 7 π
P i = P 0
Now since it is a polytropic process V P = K
V i P i = V a i r P a i r
Hence we have :
P a i r = 3 7 8 ( 1 − x ) ( x 2 + 4 x + 7 ) P 0
Writing bernoulli equation for the given two points (one is a point at the junction and
another point is just outside the hole) we have :
P a i r + ρ g x + 2 1 ρ v 1 2 = P 0 + 2 1 ρ v 2 2
v 1 = velocity of water level
v 2 = velocity of water coming out of hole :
Also using equation of continuity we have :
A 1 v 1 = A 2 v 2
A 1 = Area of junction( of air and water ) = π ( 1 + x ) 2
A 2 = Area of hole
Solving we get the expression of v 1 as :
( ( A 2 A 1 ) 2 − 1 ) v 1 2 = ρ 2 ( P a i r − P 0 ) + 2 g x
Putting the values we have :
( 1 0 4 π 2 ( 1 + x ) 2 − 1 ) v 1 2 = 2 0 0 ( 3 7 8 ( 1 − x ) ( x 2 + 4 x + 7 ) − 1 ) + 2 0 x
Note that − d t d x = v 1
Finally I get the expression of T as :
∫ 1 / 4 1 / 2 2 0 x + 3 7 2 0 0 ( 8 ( 1 − x ) ( x 2 + 4 x + 7 ) − 3 7 ) 1 0 4 π 2 ( 1 + x ) 4 − 1 d x = 2 6 . 2 5 6 4