Water Depth in an Ellipsoidal Tank
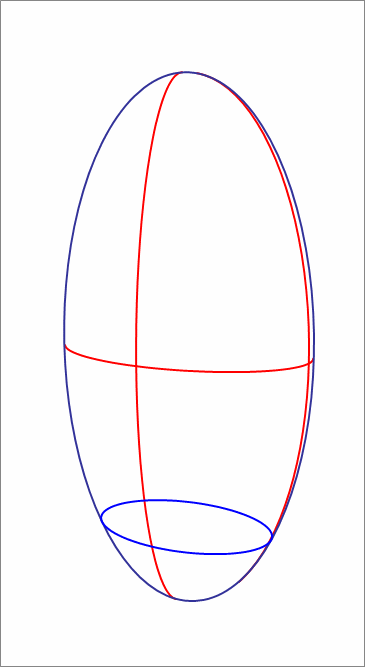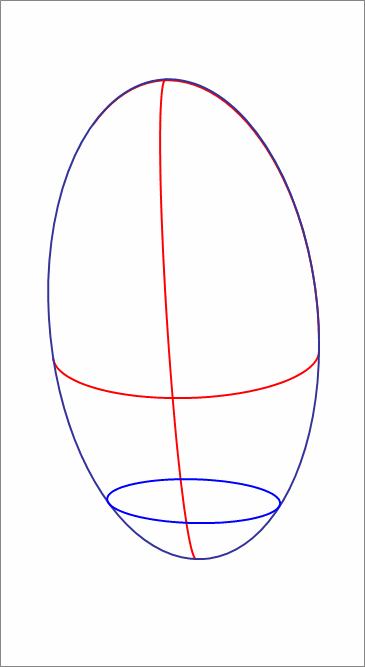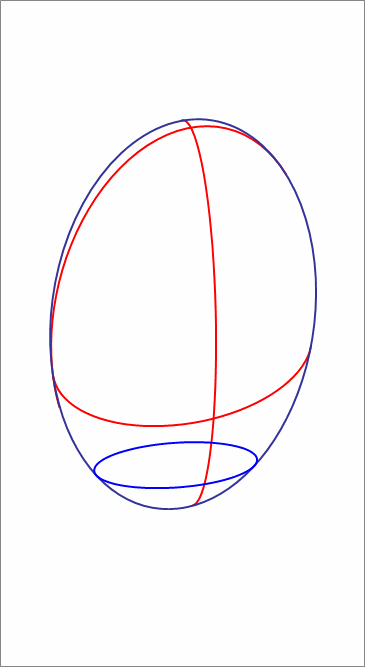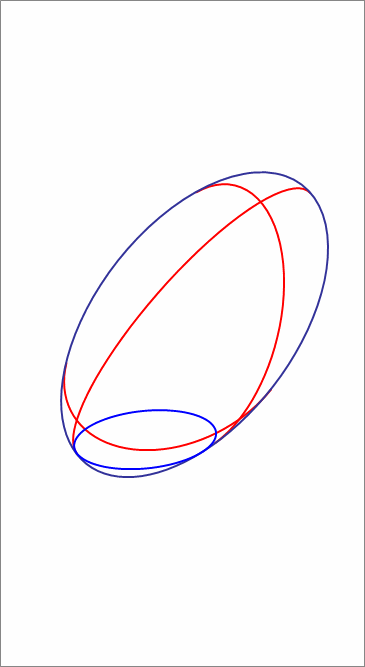
A water tank in the shape of an ellipsoid with semi-axes of lengths 5 0 cm , 1 0 0 cm , 3 0 0 cm is placed on a floor such that it stands 6 meters high (that is, the third axis is perpendicular to the floor).
Water is poured into the tank to a height of 1 4 4 cm . Then the water tank is tilted and rotated such that the difference in elevation between the highest point of the ellipsoid and the lowest point is 4 meters.
What is the new depth of water in the tank ( in cm ) ?
The animation attached depicts the situation.
The answer is 96.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let y 0 be the height of the highest point above the lowest point; y the height to which the ellipsoid is filled; V 0 the volume of the ellipsoid; and V the volume of the fluid. Then V 0 V = f ( y 0 y ) , where f ( ⋅ ) is a function independent of the shape and orientation of the ellipsoid. ( ⋆ )
Thus, if V ′ / V 0 ′ = V / V 0 , then y ′ / y 0 ′ = y / y 0 and y ′ = y ⋅ y 0 y 0 ′ = 1 4 4 c m ⋅ 6 m 4 m = 9 6 c m .
Proof of claim ( ⋆ ) above.
An ellipsoid (centered at the origin) is obtained by linear transformation of the unit sphere. Rotating the ellipsoid is also a linear transformation. So any ellipsoid can be written in the form ⎝ ⎛ x y z ⎠ ⎞ = T ⎝ ⎛ x 0 y 0 z 0 ⎠ ⎞ , where T is a 3 × 3 -matrix and x 0 , y 0 , z 0 are points on the unit sphere. In fact, using the rotational freedom of the unit sphere, we can write T in the form T = ⎝ ⎛ a c 0 b d 0 u v h ⎠ ⎞ . Since z = h z 0 , it is obvious that the highest and lowest points of the ellipsoid are ± h . Also, its volume is V 0 = 3 4 π det T = 3 4 π h ( a d − b c ) . Intersecting the unit sphere at height z 0 results in a circle C 0 ( z 0 ) with area A 0 ( z 0 ) ; likewise, intersecting the transformed unit sphere at height z = h z 0 results in a linearly transformed circle (i.e. ellipse) C ( z ) defined by ( x y ) = ( a c b d ) ( x 0 y 0 ) + ( u v ) ; its area is A ( z ) = A 0 ( z 0 ) det ( a c b d ) = A 0 ( z / h ) ( a d − b c ) .
If the unit sphere is filled from the lowest level z 0 = − 1 to a given level z 0 ′ , the volume of the liquid is ∫ − 1 z 0 ′ A 0 ( z 0 ) d z 0 = : v ( z 0 ′ ) . Likewise, when the ellipsoid is filled to level z ′ = h z 0 ′ , V = ∫ − h z ′ A ( z ) d z = ∫ − h z ′ A 0 ( z / h ) ( a d − b c ) = h ∫ − 1 z ′ / h A 0 ( z 0 ) ( a d − b c ) d z 0 = h ( a d − b c ) v ( z ′ / h ) , and V 0 V = 3 4 π h ( a d − b c h ( a d − b c ) v ( z ′ / h ) = 4 π / 3 v ( z ′ / h ) . The latter expression is equivalent to f ( y / y 0 ) in the discussion above.
Yes, but you need to justify your statement about the relation between V 0 V and y 0 y .
Log in to reply
I will do that. See my solution.
Log in to reply
I look forward to your solution, but meanwhile I've published my own solution.
Thanks for posting a detailed solution.
This is a very interesting problem. The solutions provided by Hosam Hajjir and Arjen Vrengdenhil are excellent and in-depth.
First, check out Afffine Transforms , which is really at the heart of this problem.
This will be an effort at a brief, if incomplete, proof (or explanation). Consider three ellipsoids, all of them having the same height of 4 0 0 c m from floor to top, and same volume. The first has a vertical axis and circular cross sections perpendicular to that axis, the radius of the midsection circle being 5 0 3 . The second similarly has a vertical axis and elliptical cross sections perpendicular to that axis, the major and minor axes of the midsection ellipse being 1 0 0 3 2 and 5 0 3 2 . The last is the tilted ellipsoidal tank. The second is the original upright tank that has been "squeezed" into a shorter and wider tank of the same volume, using an affine transform.
At any given height on the vertical axes, the area of the cross section of both the 1 s t and 2 n d tanks are the same. If it can be shown that the 3 r d tank can be obtained from the 1 s t by an affine transform limited to the planes perpendicular to the axes, then the area of the cross section of both the 1 s t and 3 r d tanks are the same. Hence, the area of the cross sections of both the 2 n d and 3 r d tanks are the same as well. Hence, a given volume water in the 3 r d tank will be of the same depth as the same volume of water in the 2 n d tank. From this, we can deduce that if a volume of water in the original upright tank has a depth of 1 4 4 , then the same volume of water in the 3 r d tank will have a depth of 3 2 ⋅ 1 4 4 = 9 6
Suppose an afffine transform (limited to the planes perpendicular to the axes) obtains the 3 r d ellipsoid from the 1 s t . Then all of the elliptical cross section areas of the 3 r d ellipsoid corresponding to the circular cross sections of the 1 s t ellipsoid will have the same eccentricity, and thus the the areas will differ by a factor that is a constant. However, for both the 3 r d and 1 s t ellipsoids to have the same volume, this constant has to be 1 . Hence the corresponding cross section areas are the same.
This not a substitution for a rigorous proof as how Hosam or Arjen has done it, but hopefully it would serve as a visual explanation of how this works. Here, two separate affine transforms were used, instead of a single general 3D affine transform.
A great variety of mathematical problems can successfully analyzed using affine transforms, a very useful tool to have.
Let's take the center of the ellipsoid to be the origin of the reference frame O x y z , and assume that the water level is at z = z 0
that is, the equation of water surface (a plane) is z = z 0
the equation of a general ellipsoid of arbitrary orientation is given by r T R D R T r = 1
where D is a diagonal matrix whose diagonal entries are the reciprocals of the squares of the semi-axes of the ellipsoid, and R is a rotation matrix.
We will now transform this ellipsoid into a sphere of unit radius by applying the following transformation
r = T r ′ = R D − 1 / 2 r ′ , i.e. r ′ = D 1 / 2 R T r
Now the original equation of the water surface is
k T r = z 0
where k = [ 0 , 0 , 1 ] T is the unit vector along the z-axis.
Applying the transformation, we get, in terms of the new coordinate r',
k T R D − 1 / 2 r ′ = z 0
Now, the signed distance of this plane to the center of the unit sphere is
d = z 0 / k T R D − 1 R T k = z 0 / h
One can show that k T R D − 1 R T k is the maximum elevation of the ellipsoid above the center. To show this, consider a horizontal plane touching the ellipsoid from above,
then the gradient of ellipsoid at the touching point r 1 will be parallel to the unit vector k ,
i.e. R D R T r 1 = α k with α > 0
therefore, r 1 = α R D − 1 R T k
plugging this into the equation of the ellipsoid , we obtain
r 1 T R D R T r 1 = 1 , so α 2 k T R D − 1 R T k = 1
hence, α = k T R D − 1 R T k 1
The elevation of r 1 is given by k T r 1 = α k T R D − 1 R T k = k T R D − 1 R T k k T R D − 1 R T k = k T R D − 1 R T k
which is what we wanted to show.
now the volume of the transformed space occupied by water in the unit sphere depends only on d. It is given by
V = π ( 2 / 3 + d − d 3 / 3 )
Therefore, from transformation theory, the volume of water in the original ellipsoid is
V = ∣ T ∣ π ( 2 / 3 + d − d 3 / 3 ) = ∣ D − 1 ∣ π ( 2 / 3 + d − d 3 / 3 )
Since the volumes in both cases are equal, then d must be equal because taking the derivative of V with respect to d, we obtain,
V ′ ( d ) = ∣ D − 1 ∣ π ( 1 − d 2 )
since d < 1 , the function is strictly increasing with d.
Hence V 1 = V 2 implies d 1 = d 2 .
thus, h 1 z 1 = h 2 z 2 .
and therefore, by adding 1 to both sides, we obtain, h 1 ( z 1 + h 1 ) = h 2 ( z 2 + h 2 )
That is, h 1 ( z 1 − ( − h 1 ) ) = h 2 ( z 2 − ( − h 2 ) ) , which translates also, into, 2 h 1 ( z 1 − ( − h 1 ) ) = 2 h 2 ( z 2 − ( − h 2 ) )
but ( z 1 − ( − h 1 ) ) is the depth of water in the first orientation of the ellipsoid, and ( z 2 − ( − h 2 ) ) is the depth of water of the second orientation of the ellipsoid, hence
( z 2 − ( − h 2 ) ) = 2 h 1 2 h 2 ( z 1 − ( − h 1 ) ) = 6 4 ( 1 4 4 ) = 9 6 cm
'