Water in a straw

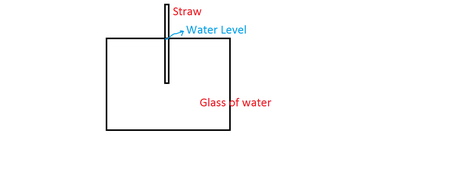
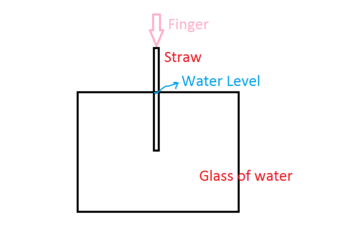
When we seal the top end of the straw with a finger then the air gets trapped in the upper portion. The trapped air has the pressure equal to the atmospheric pressure that is $P_0$ . Now, if the straw is taken out then the pressure difference above and below the water is equal and no force is available to carry the weight of the water. Thus, the water in the straw falls down.

However, as the water level falls, the trapped air expands which will result in a decrease in its pressure. This leads to a pressure difference of $\Delta P$ across the water column. Eventually, the system will attain an equilibrium where the force due to this pressure difference equals the weight of the water remained in the straw.

Bonus:

Calculate the height up to which the water will remain in the straw. Given the atmospheric pressure is $P_0$ , the density of water is $\rho$ , the total height of the straw is $h$ and the acceleration due gravity is $g$ . Assume that the temperature of the trapped air remains constant.

This is what my concept says. Firstly, When we dip the straw. We get something like this

Now see, When we put our hand on the top (Or finger)

Now see we have blocked the place for air to move in when we take out the straw.

So when we start taking the straw out and when we completely bring it out and hold it with our finger,

Then the little water inside falls and the rest of the water in the straw moves up to take the place of the air. This is what is the phenomenon happening,

Am i correct?

Do not agree with explanation of Rohit.. All that formula will be applicable till the bottom end remains inside water. The moment you take it out, the atmospheric air will displace the water in straw (no more physics)...