water in the basin
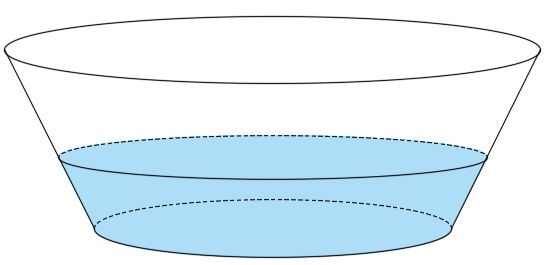 A basin made of plastic has an upper base diameter of 30 cm, a lower base diameter of 20 cm and a height of 10 cm. It is filled with water at a height of 4 cm. How much area of the basin (in square cm) is wet?
A basin made of plastic has an upper base diameter of 30 cm, a lower base diameter of 20 cm and a height of 10 cm. It is filled with water at a height of 4 cm. How much area of the basin (in square cm) is wet?
Note: Neglect the thickness of the basin.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
From the similar triangles on the left side, we get 4 x = 1 0 5 ⟹ x = 2 ⟹ R = 1 2 .
The wet area is the area of the lower base and the curved surface area of the frustum ; the latter's formula is π ( R + r ) ( R − r ) 2 + h 2 .
Thus the wet area is
π ( R + r ) ( R − r ) 2 + h 2 + π r 2 = π ( 1 2 + 1 0 ) ( 1 2 − 1 0 ) 2 + 4 2 + π ( 1 0 2 ) = 4 4 5 π + 1 0 0 π