Water Level in a Tank

Classical Mechanics Level 3

Consider a tank of a cross-sectional area of A (when viewed from the top). Water flows into this tank from the top at a volumetric flow rate of $Q$ . The tank has a hole at the bottom which can be opened or closed by a valve. At time $t=0$ the valve opens allowing water to flow out. The area of this hole at the bottom is $A_o$ . What is the height of the water level (in meters) in the tank four minutes after the valve opens? Assume that the tank is empty when the valve just opens.

Notes and assumptions:

$A = 0.15 \ m^2$ , $Q = 0.005 \ m^3/s$ , $A_o = A/100$ , $g = 10 \ m/s^2$
$A_o<<A$ holds true
The cross sectional area of the tank remains constant throughout its height.
There are no ambient pressure variations throughout the height of the tank.

Bonus: Is a steady-state height attained? If yes, what is it? State your conclusions based on this.

The answer is 0.5553.

2 solutions

Uros Stojkovic
May 12, 2020

We're expected to model the evolution of the system by the following equation: $\begin{aligned} \dot{V} &= Q - A_{0}v_{hole} \\ A\dot{h} &\approx Q - A_{0}\sqrt{2gh}\end{aligned}$ The integral of this equation is: $t + \frac{A}{A_{0}}\sqrt{\frac{2h}{g}} + \frac{QA}{gA_{0}^{2}}\ln(Q - A_{0}\sqrt{2gh}) = \text{const.}$ When we plug in initial conditions, it becomes: $t + \frac{A}{A_{0}}\sqrt{\frac{2h}{g}} + \frac{QA}{gA_{0}^{2}}\ln{\left(1 - \frac{A_{0}}{Q}\sqrt{2gh} \right )} = 0.$

However, I believe that this is not the most accurate model because we used Torricelli's law which is derived from the standard form of Bernoulli equation. Here the problem arises, I think, because the Bernoulli equation is valid only when the fluid flow is steady i.e. doesn't depend on time, which here obviously isn't the case. Mathematically, the Newton's second law for a small fluid parcel is: $\begin{aligned} &dm\,\vec{a} = -\oiint p\,\vec{dA} + dm\,\vec{g} \\ &\rho\vec{a} = -\nabla p - \nabla(\rho gh) \\ &\rho\vec{a} +\nabla p + \nabla(\rho gh) = 0,\end{aligned}$ Bernoulli equation, which is the simple integral of the above equation, can be obtained and interpreted correctly only when the flow is steady.

I must admit, though, that I'm not completely sure about the correctness of my analysis either.

Thank you for the solution. To address your point on your analysis, the following are my thoughts.

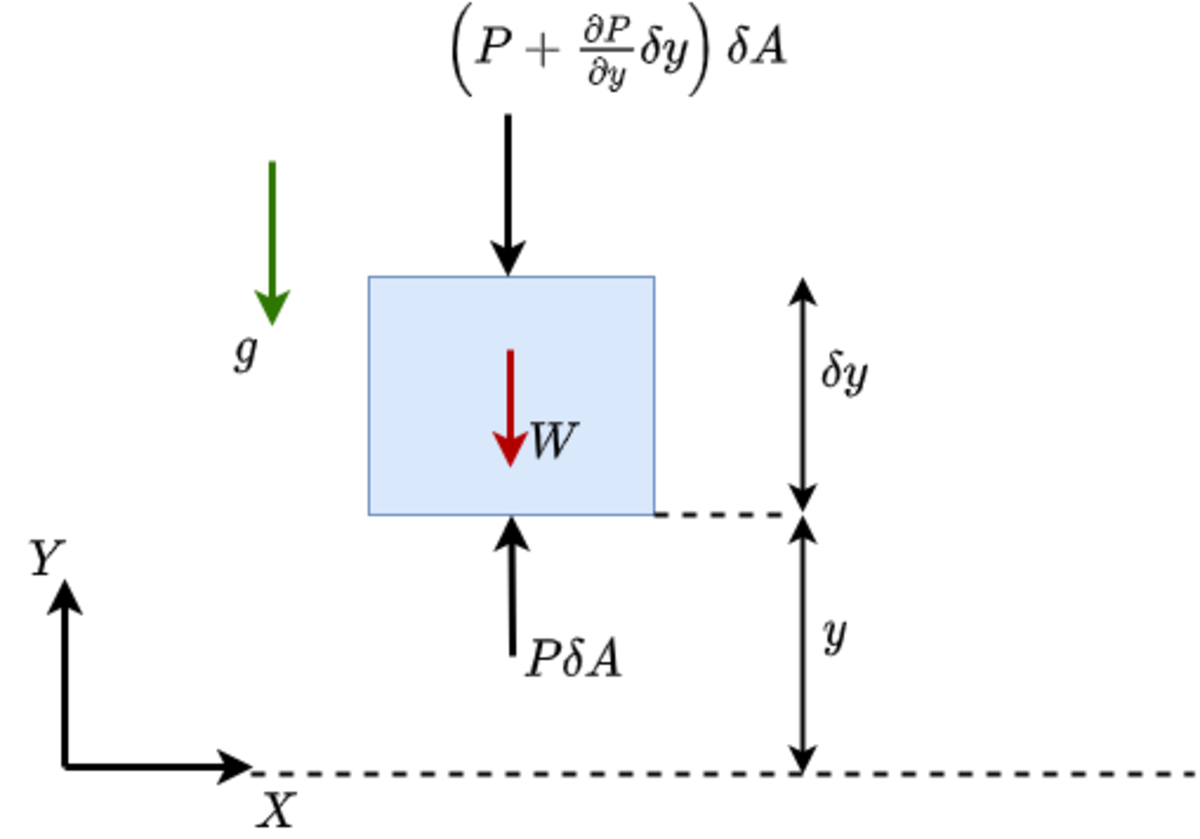
Think of vertical fluid flow. The fluid is incompressible. Consider an element of fluid within that continuum. The forces acting on that element are shown in the diagram above. Let the volume of the element be $\delta V = \delta y \ \delta A$

Applying Newton's second law:

$\delta V \rho a_y = -\frac{\partial P}{\partial y} \delta y \ \delta A - \delta V \rho g$ $\implies \rho a_y= -\frac{\partial P}{\partial y} -\rho g$

Now From the chain rule, it follows that:

$a_y = v_y\frac{\partial v_y}{\partial y}$

$\implies \rho v_y\frac{\partial v_y}{\partial y}= -\frac{\partial P}{\partial y} -\rho g$

The partial derivatives get converted to regular derivatives as $y$ is the only variable above. This gives:

$\rho v_y \ dv_y = -dP -\rho g \ dy$

Integrating gives:

$P + \rho g y + \frac{1}{2}\rho v_y^2=C$

This is the bernoulli's equation. Nowehere in the derivation here have I assumed that flow is steady. So your statement about steady flow is not true.

Bernoulli's equation does hold for non-steady fluid flow. The assumptions made to derive Bernoulli's equations are:

Fluid volume is continuous
Fluid is incompressible
Flow is laminar
Flow along a single stream is considered. So the equation hold true for a single stream of fluid.

I have derived this equation for the more specific case of vertical flow in a tank. But this derivation can be easily generalised.

Karan Chatrath - 1 year, 1 month ago

Actually you have assumed that the flow is steady. In general, we have: $\vec{a} = \frac{\mathrm{d} \vec{v}}{\mathrm{d} t} = \nabla \vec{v}\,\cdot \vec{v} + \frac{\partial \vec{v}}{\partial t},$ or considering only spatial component $y$ : $a_{y} = \frac{\mathrm{d} v_{y}}{\mathrm{d} t} = \frac{\partial v_{y}}{\partial y}\,v_{y} + \frac{\partial v_{y}}{\partial t}.$ However, you omitted this last term which captures explicit time dependence of the flow and by doing so you implicitly assumed that the flow velocity is a function of spatial coordinates only - characteristic of the steady flow. The Wikipedia article also states that classical form of Bernoulli equation demands steady flow. Here's one interesting MIT paper I've found which considers unsteady flow.

Uros Stojkovic - 1 year, 1 month ago

You are right. I stand corrected. I feel silly to have made such a mistake. Now I think that your argument is valid and that the use of Toricelli's law is not the most accurate model. It really makes me think about this formulation now. Cause problems on emptying tanks usually make the assumption that Toricelli's law is valid.

Karan Chatrath - 1 year, 1 month ago

Don't feel silly! I guess they employ Torricelli's law because of the simplicity of the solution. Without the steady flow assumption, it seems to me that analysis becomes pretty complicated.

Uros Stojkovic - 1 year, 1 month ago

Steven Chase
Dec 8, 2019

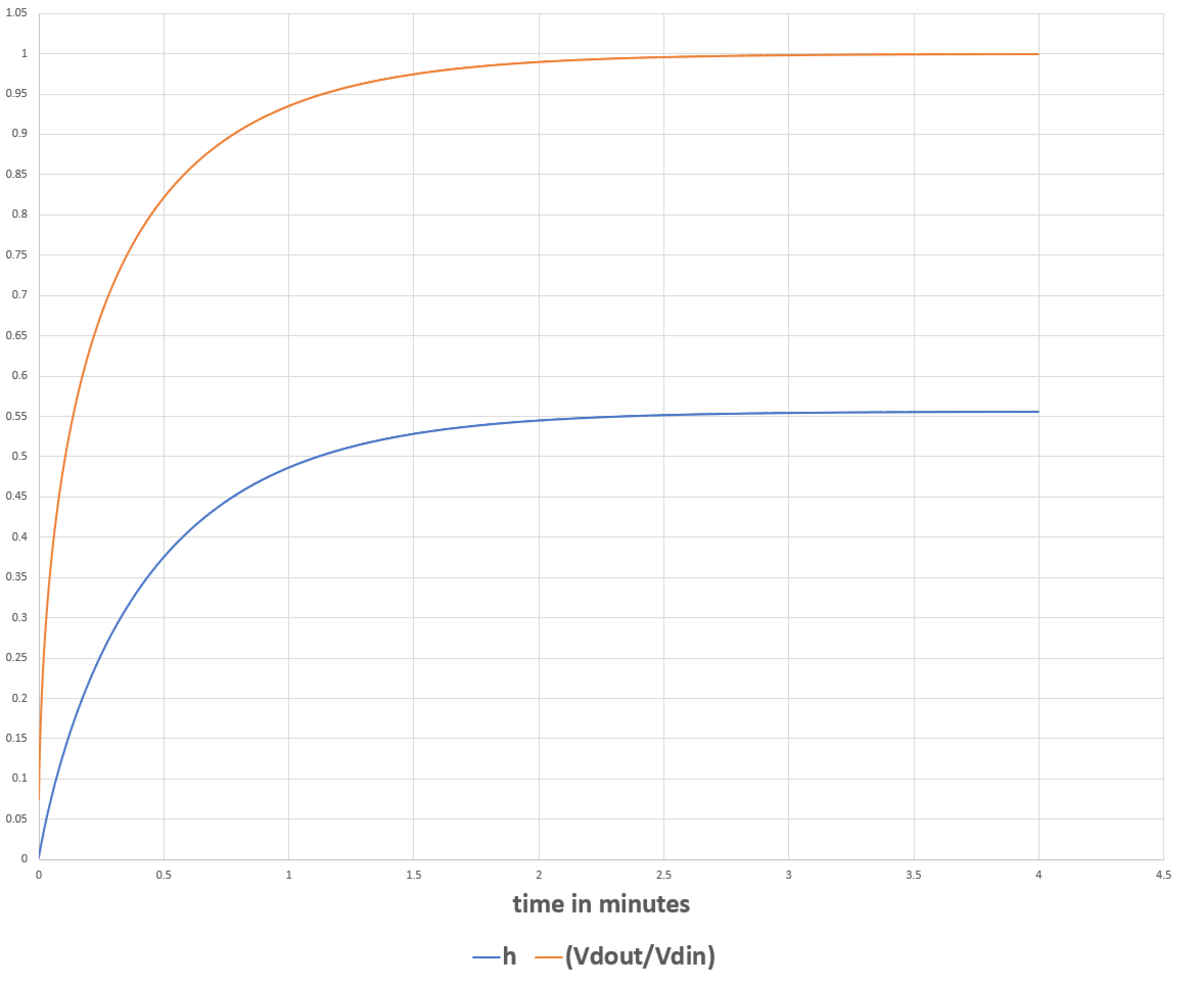
The height will asymptotically approach a steady state as the output valve flow rate approaches the input flow rate. After four minutes, the tank has more or less reached this steady-state height. Simulation code is below, as well as a plot of height over time, alongside the ratio of output flow rate to input flow rate.

import math

# Constants

A = 0.15
Q = 0.005
A0 = A/100.0
g = 10.0

dt = 10.0**(-5.0)

min = 60.0

#################################

# Initialize variables

V = 0.0   # volume
Vd = Q    # volume rate of change

t = 0.0
count = 0

#################################

# Run simulation

print "(t/min) h (Vdout/Vdin)"

while t <= 4.0*min:

    V = V + Vd * dt   # numerical integration

    h = V/A           # water height

    u = math.sqrt(2.0*g*h)  # flow speed out of valve - Toricelli

    Vdout = A0*u   # outward flow rate
    Vdin = Q       # inward flow rate

    Vd = Vdin - Vdout  # net flow rate

    t = t + dt
    count = count + 1

    if count%10000 == 0:
        print (t/min),h,(Vdout/Vdin)

#################################

print ""
print ""

print h

Water Level in a Tank

The answer is 0.5553.

2 solutions

0 pending reports