Water planet
A tiny planet is made entirely of water and is held together only by its own gravity. At the center of the planet there is a pressure p 0 = 2 4 bar = 2 . 4 MPa . What is the radius R of the planet in kilometers? Round the result to the nearest integer.
Assumptions: The density ρ 0 = 1 0 0 0 kg / m 3 of the water is homogeneous. The planet has the shape of a perfect sphere. The planet does not rotate around its own axis and has no water flow.
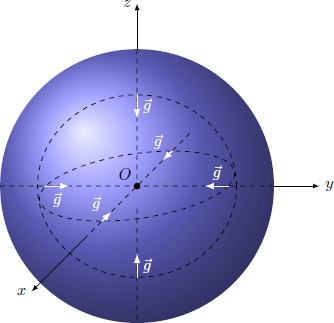
Hints: The gravitational pressure is determined by the differential equation ∇ p ( r ) = ρ 0 g ( r ) with the boundary condition p = 0 at the surface and the gravitational acceleration g ( r ) . Analogous to electrostatics, Gauss's law can also be formulated for gravitation: ∮ g ( r ) ⋅ d A = − 4 π G ∫ ρ ( r ) d V with gravitation constant G = 6 . 6 7 3 ⋅ 1 0 − 1 1 kg m 3 s 2 .
Bonus problem: Estimate the pressure in earth's center. The earth has an average density of ρ E ≈ 5 5 0 0 kg / m 3 and a radius R E ≈ 6 6 0 0 km .
The answer is 131.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
This actually comes out to 131.04...., so rounding to the next integer gives 132
Log in to reply
I changed now the word "next" to "nearest". But honestly, the exakt result is almost already an integer, so that only very few would come up with the idea to round up ..., or not?
But in rocket science 131 would be the next integer xD
Due to spherical symmetry, the fields g ( r ) = g ( r ) e r and p ( r ) = p ( r ) depend only on radial distance r = ∣ r ∣ and the unit vector e r = r / r . If we integrate over a sphere with radius r ≤ R , Gauss' law results ∮ g ( r ) ⋅ d A − 4 π G ∫ ρ ( r ) ⋅ d V ⇒ g ( r ) = g ( r ) ⋅ 4 π r 2 = − 4 π G ρ 0 ⋅ 3 4 π r 3 = − 3 4 π G ρ 0 r Integration of the differential equation determines the gravitational pressure: ∇ p ( r ) ⇒ p ( r ) = ∂ r ∂ p = ∂ r ∂ p ∂ r ∂ r = p ′ ( r ) ⎝ ⎛ x / r y / r z / r ⎠ ⎞ = p ′ ( r ) e r = ρ 0 g ( r ) e r = ∫ 0 r ρ 0 g ( r ) d r + p 0 = − 3 2 π G ρ 0 2 r 2 + p 0 Since p ( R ) = 0 , the pressure in the center of the planet results p 0 ⇒ R = 3 2 π G ρ 0 2 R 2 = 2 π G ρ 0 2 3 p 0 ≈ 1 3 1 km