Water pump problem
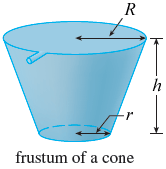
Assume , , and tank is filled with water. Find the work required to pump all water out of the spout.
Water weighs .
Answer in .
The answer is 1872590.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We can write radius of a sliced cross section of the frustum as r + h ( R − r ) ∗ x as a function of x, Hence
Area of circles formed as a function of x is = π ∗ ( r + h ( R − r ) ∗ x ) 2
Now integrating area of circles of radius given by this function with bounds h and 0 gives the volume . ∫ 0 h π ∗ ( r + h ( R − r ) ∗ x ) 2 d x , substituting r=6 ,R=12 and h=17, and multiplying with weight density we get force acting on each differential volume of water. ∫ 0 h 6 2 . 5 ∗ π ∗ ( 6 + 1 7 6 ∗ x ) 2 d x
Now Consider a differential volume of the frustum at x, this volume must be lifted (17-x) distance. We have Force = ∫ 0 h 6 2 . 5 ∗ π ∗ ( 6 + 1 7 6 ∗ x ) 2 d x and displacement equals (17-x),
W= ∫ 0 h ( 1 7 − x ) ∗ 6 2 . 5 ∗ π ∗ ( 6 + 1 7 6 ∗ x ) 2 d x definite integral from 0 to h=17 gives 1872590 lb-ft.