water volume

Geometry Level 3

a cylinderical tank is fixed horizontally for water storage as shown on figure , the tank is filled with water up to a maximum depth of 1.50 m. if the volume of water ( in m 3 m^3 ) is a π + b √ 3 3 \frac{aπ + b√3 }{3} , where a and b are positive integers find a + b .


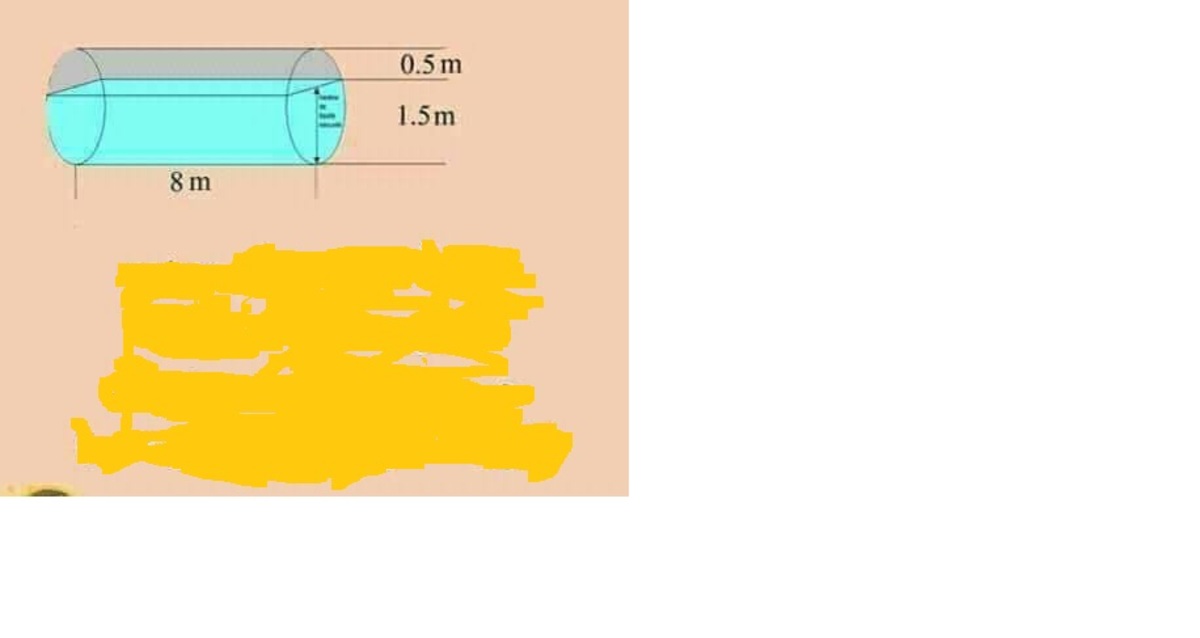
The answer is 22.

Aziz Alasha by Aziz Alasha , 59, Sudan

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Tom Engelsman
Sep 6, 2017

The water's cross-sectional area is comprised of a 240-degree circular sector (radius = 1) and a isosceles triangle (base = 3 \sqrt{3} and height = 1 2 \frac{1}{2} ). The entire volume is computed to be:

V = B h = [ 1 2 ( 1 2 ) ( 4 π 3 ) + 1 2 ( 1 2 ) ( 3 ) ] ⋅ 8 = [ 2 π 3 + 3 4 ] ⋅ 8 = 16 π + 6 3 3 . V = Bh = [\frac{1}{2}(1^2)(\frac{4\pi}{3}) + \frac{1}{2}(\frac{1}{2})(\sqrt{3})] \cdot 8 = [\frac{2\pi}{3} + \frac{\sqrt{3}}{4}] \cdot 8 = \boxed{\frac{16\pi + 6\sqrt{3}}{3}}.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...