Waterflow Problem
The array
2 5 3 4 3 2 5 5 3 4 2 2 2
represents the hill below.
If it rains in the hill, 9 units of water accumulate. (Water is assumed to run off the edges.)
Given the hill represented by the array below, how many units of water will accumulate?
hill = [4, 2, 4, 1, 5, 3, 16, 6, 17, 19, 4, 13, 5, 3, 10, 10, 13, 6, 2, 1, 5, 15,
13, 19, 16, 9, 13, 1, 7, 18, 20, 13, 9, 7, 2, 10, 8, 18, 4, 7, 5, 8, 10, 13,
7, 18, 19, 2, 19, 8, 10, 10, 17, 6, 6, 20, 20, 11, 10, 11, 13, 9, 7, 1, 10,
5, 12, 16, 10, 7, 15, 13, 12, 10, 1, 1, 4, 2, 16, 10, 20, 17, 11, 19, 19, 20,
9, 10, 17, 9, 18, 8, 10, 18, 8, 19, 16, 17, 3, 1]
The answer is 791.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
36 solutions
You did this by hand?
Log in to reply
I did it in Excel. Four formulas, some copying.
Log in to reply
Nice. There is a cute translation of the same thing into Haskell, which I posted in another solution,
I did it by hand. I would have used google sheets but didn't know the easy way to put one number in each cell.
Log in to reply
I also did this by hand, however I didn't use google sheets or Microsoft Excel. I literally drew this out my hand. As a person who doesn't know python well enough to solve this, I believe I'm gonna need to learn how to use python. Good luck.
Can you please explain mathematically or pictorially?Please do not explain using python,because I do not know it.
This sooooooo elegant
Can you show that mathematically or as a program which is not Haskell?
Log in to reply
here is a code which works in Sagemath (its basically python with a few other functions). It's just one line ;o) I adapted (and commented) the code to python in an answer below if you want to look this up.
1 |
|
hill = [4, 2, 4, 1, 5, 3, 16, 6, 17, 19, 4, 13, 5, 3, 10, 10, 13, 6, 2, 1, 5, 15,
13, 19, 16, 9, 13, 1, 7, 18, 20, 13, 9, 7, 2, 10, 8, 18, 4, 7, 5, 8, 10, 13,
7, 18, 19, 2, 19, 8, 10, 10, 17, 6, 6, 20, 20, 11, 10, 11, 13, 9, 7, 1, 10,
5, 12, 16, 10, 7, 15, 13, 12, 10, 1, 1, 4, 2, 16, 10, 20, 17, 11, 19, 19, 20,
9, 10, 17, 9, 18, 8, 10, 18, 8, 19, 16, 17, 3, 1]
v1=0
saved=0
for i in range(0,len(hill)):
v1=hill[i]
vf=0
vb=0
maxi=0
for j in range(i,len(hill)):
if hill[j] > maxi:
maxi=hill[j]
vf=maxi
maxi=0
j=i
while j>=0:
if hill[j] > maxi:
maxi=hill[j]
j+=-1
vb=maxi
v=min(vf,vb)
saved+=max(0,v-v1)
print(saved)
This Is The code That Does so .

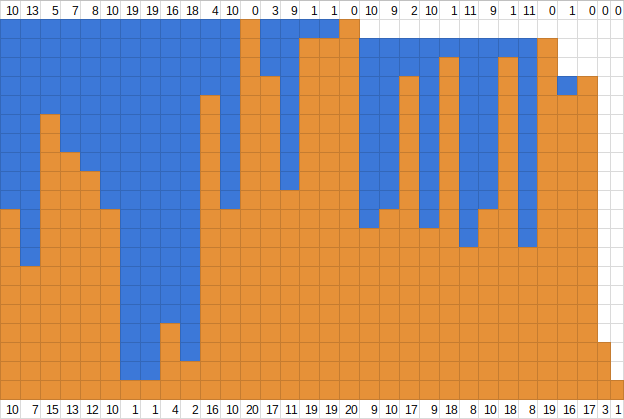
The bottom row is the array, and the top row is the number of cells with water in each column. If you add all the numbers in the top row, you will get that the total amount of water is 791.
Great job on a pictorial solution. How did you produce this image?
The array got truncated on my iPad. Feeling disgruntled.
Here is a beautiful implementation of what @Marta Reece said, in Haskell:
1 2 3 4 5 6 7 |
|
I have a small query. I would appreciate some help. I tried implementing the following algorithm in python , but it doesn't give the correct answer in some cases. Can you tell me what is going wrong?
Let's call the array L. If len (L) <= 2 , we would return 0. So , suppose len (L) > 2.
Let x and y be the indices of the largest and second largest element of L (they may be same). Note that , in case , there are many elements which are the largest , we choose the one with the smallest index.
We calculate the water stored between x and y. That will be given by : S = (len(A))*(L[y]) - sum(A) where , A = [ L[k] for k in range(1+ min(x,y) , max(x,y)) ]
Then , we calculate water stored for the array L[ : ((min(x,y))+1)] and L[ max(x,y) :] and add both with S. Hence , recursively we should get the answer for L.
Log in to reply
Here's my python implementation:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
|
Log in to reply
How do you accumulate more water than you put in? I was under the impression that 9 units of water went in. Please clarify the question. It is too vague.
Come on , answer is 51
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
|
Here's a really short python solution:
hill = "4 2 4 1 5 3 16 6 17 19 4 13 5 3 10 10 13 6 2 1 5 15 13 19 16 9 13 1 7 18 20 13 9 7 2 10 8 18 4 7 5 8 10 13 7 18 19 2 19 8 10 10 17 6 6 20 20 11 10 11 13 9 7 1 10 5 12 16 10 7 15 13 12 10 1 1 4 2 16 10 20 17 11 19 19 20 9 10 17 9 18 8 10 18 8 19 16 17 3 1"
hill_nums = [int(x) for x in hill.split(" ")]
water = [0] * len(hill_nums)
print(water)
for i in range(1, len(hill_nums)-1):
water[i] = max(0, min(max(hill_nums[:i]), max(hill_nums[i+1:])) - hill_nums[i])
print(water)
print(sum(water))
Short and sweet. But where is the output?
I only got the numbers 1-the second 13 SL my answer ended up being wrong, but I triple checked each time getting the same answer of 50. Is this right? And I drew it out because I can't do code.
Just a reminder: split() splits by space by default, no need to split(" ")
Fed 100 and the array to STDIN.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
|
So you need to make a new array in which the values of the current array are replaced by the minimum of "maximum of the previous entries" and "maximum of the upcoming entries". This minimum gives the water level. You then need to subtract the hill level to have the water content, and then sum it all to get the total water content.
Here is my one line solution ;o) (well actually is two lines because I need to import numpy)
1 2 |
|
It returns 7 9 1 .
details:
max(hill[0:i+1])
and
max(hill[i:len(hill)])
return "maximum of the previous entries" and "maximum of the upcoming entries"
min(max(hill[0:i+1]),max(hill[i:len(hill)]))
is the water level at the i
th
entry.
min(max(hill[0:i+1]),max(hill[i:len(hill)])) - hill[i]
is the water content corresponding to this entry.
[ "some expression with i" for i in range(0,len(hill))]
makes a list with the same length as hill and the i
th
entry is evaluated. So in our case the list of the water content at the current position.
np.sum()
returns the sum of the list elements. So in our case the total water content.
Here's the same in one line (using the built-in sum instead of numpy's sum) :):
print(sum([min(max(hill[0:i+1]), max(hill[i:len(hill)])) - hill[i] for i in range(1,len(hill))]))
Log in to reply
Strange, I remember that when I tried to run this (without importing numpy) in the shell provided by the website it didn't work (it did work on my PC though). I needed to import numpy to make it work here. But now it apparently runs without importing numpy... stange...
Anyway, thanks for the info!
For each point take the lesser of the left and right highest peaks (aka water level) and subtract the hill height.
In python:
f o r i i n r a n g e ( l e n ( h i l l ) ) : w a t e r + = m i n ( m a x ( h i l l [ : i + 1 ] ) , m a x ( h i l l [ i : ] ) ) − h i l l [ i ]
Note: The +1 is neccesary since a[b:c] includes b but excludes c. Therefore "hills up to and including i" is "hill[:i+1]" while "hills from and including i" is just "hill[i:]".
I did it in steps manually. Let the first largest and the second largest numbers are n and m respectively. They could be equal. If they repeat, use the left most and the right most numbers. To complete the step find the differences of m(second largest) and any number between the two chosen largest numbers. Now find the total of all differences. The total is the result of the step. Repeat the step to the left and to the right of the chosen numbers till all numbers are covered. If there aren't numbers between the two chosen numbers, the result of the step is 0. I did it in 10 steps. Lastly find the sum of the results from all of the steps. You should end up with 791.
Step 1: The two largest numbers are 20 and 20, result 512. The steps on the left side of 20 and 20 are with numbers: 19 and 20, result 197: 17 and 19, result 0; 16 and 17, result 10; 5 and 16, result 2; 4 and 5, result 5. On the right side of the initial numbers 20 and 20 the steps are with numbers: 20 and 19, result 64; 19 and 17, result 1; 17 and 3, result 0; 3 and 1, result 0. As I said, we end up with 791.
Very nice.
In Python 3. Gives the answer 7 9 1 .
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
|
This solution focuses on rows rather than columns. Implemented in MATLAB.
Let x be the m -dimensional vector that describes the cell topography. Transform x into an n × m binary matrix where 1 and 0 represent land and sky respectively. Note that n = max x . For the i t h row in this matrix (where i = 1 , . . . , n ), trim the leading and trailing zeros to create a new vector, y i . Then the water in the i t h row is equal to l e n g t h ( y i ) − s u m ( y i ) and the total water is then ∑ i = 1 n ( l e n g t h ( y i ) − s u m ( y i ) ) .
Here's a visual of the example.
The MATLAB code. It could be tightened up a bit, of course.
This makes way more sense. A row-by-row approach, starting from the bottom going up, and then bounding the rows by the "land masses" and counting the empty spaces in-between is quicker and more algorithmic.
I used the same algorithm as Marta
For those who want to try, I copied the land array into cells A3:A102 (and included terminating zeroes in A2 and A103)
In cell B3 insert formula:
= M A X ( M I N ( M A X ( A $ 2 : A 2 ) − A 3 , M A X ( A 4 : A $ 1 0 3 ) − A 3 ) , 0 )
and copy down to B102.
Then sum B3:B102 to get the accumulated amount of water.
I too used the same algorithm as Marta, implementing it in Excel as did Alex Crawford. His code is more parsimonious than mine but I did include the wrinkle of having it tally the water accumulation as it progressed down the list of heights (using Alex's formulation): =B1+MAX(MIN(MAX(A$1:A2)-A2,MAX(A2:A$100)-A2),0) with B1 primed as 0. The list of heights is in column A (A1:A100) and the corresponding running sum is in column B. The correct sum is given in cell B100, as 791 units.
In R
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
|
An explanation would be helpful
I am doing a visual solution by print out the hills. Then scan each level for the first and last barriers. The empty spaces are where water exists.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
|
a little complicated solution : )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
|
A brute force solution. Scan each level of terrain. Every time you encounter a column with a block at that level, you take the distance to the previous 1 and subtract 1 (so the number of spaces between them), then overwrite the previous one as the current one. This code basically counts up the amount of water on each layer, layer by layer.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
|
Hi, i did this bottom up:
- trim the empty space surrounding the hill
- count the empty spaces and add the result to final result
- fill the empty spaces with 1
- strip the bottom layer of the hill by 1
repeat until the hill width shrunk to at least 2
python code:
import numpy as np
hill = "4 2 4 1 5 3 16 6 17 19 4 13 5 3 10 10
13 6 2 1 5 15 13 19 16 9 13 1 7 18 20 13 9 7
2 10 8 18 4 7 5 8 10 13 7 18 19 2 19 8 10 10
17 6 6 20 20 11 10 11 13 9 7 1 10 5 12 16
10 7 15 13 12 10 1 1 4 2 16 10 20 17 11 19
19 20 9 10 17 9 18 8 10 18 8 19 16 17 3 1"
.split(" ")
hill = np.array(list(map(int, hill)))
water = 0
while(len(hill) > 2):
hill = np.trim_zeros(hill)
water += np.count_nonzero(hill == 0)
hill = hill + (hill == 0)
hill = hill - 1
print(water)
Below is a Java Script code that solves this problem.
var hill = [4, 2, 4, 1, 5, 3, 16, 6, 17, 19, 4, 13, 5, 3, 10, 10, 13, 6, 2, 1, 5, 15, 13, 19, 16, 9, 13, 1, 7, 18, 20, 13, 9, 7, 2, 10, 8, 18, 4, 7, 5, 8, 10, 13, 7, 18, 19, 2, 19, 8, 10, 10, 17, 6, 6, 20, 20, 11, 10, 11, 13, 9, 7, 1, 10, 5, 12, 16, 10, 7, 15, 13, 12, 10, 1, 1, 4, 2, 16, 10, 20, 17, 11, 19, 19, 20, 9, 10, 17, 9, 18, 8, 10, 18, 8, 19, 16, 17, 3, 1]
var n = hill.length, hillterrain = '', hillslice;
while (Number(hill.join('')) > 0) {
for (i = 0, hillslice = ''; i < n; i++)
if (hill[i] > 0) {
hillslice += 'x'
hill[i]--
} else {
hillslice += ' '
}
hillterrain = hillterrain.concat(hillslice.trim()).replace(/x+/g, 'x')
}
console.log("The hill\r" + hillterrain)
console.log("Water in the hill\r")
console.log("Method 1: " + hillterrain.match(/ /g).length)
console.log("Method 2: " + (hillterrain.split(' ').length - 1))
console.log("Method 3: " + hillterrain.replace(/ /g, '•').replace(/x/g, '').length)
Basically, it builds the hill terrain slice by slice, from bottom to top (max of hill): a space for the water (light blue) and an 'x' for the solid (orange). As we care only for the water that stays in the hill, each time we build a hill slice, we trim it so that spaces left and right go away. After this, the slice will be a string which starts and ends with 'x' and will be appended to the terrain string. We will end up with a long string of 'x' and spaces, starting and ending with 'x'. The water that stays in the hill is the number of spaces in this string and this number can be obtained by various methods as the code shows.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
|
An O(N) brute force technique would be to set up markers on the left and right of the array, and move each in until you hit a local maximum just by comparing the selected value with the next value in (i.e. when each "hill" starts going downhill to the left or right). At that point, you know that regardless of whatever else is in happening in the middle, anything lower this is trapped water, kind of like a bowl. So, from the lower of the two walls, move inward, adding water until you run into a new, higher peak (and forming a potentially deeper bowl), check which of the two walls (right or left) is higher, and repeat the process. Once the point you're measuring hits the opposite wall, you've finally counted everything available.
Here's some code for it in python (written by someone who doesn't actually know python, so apologies for all the obvious shortcuts I've skipped):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
|
Here is my solution in Java:
public static int getWater (String hillString) {
String[] _hill = hillString.split(" ");
int[] hill = new int[_hill.length];
int maxValue = Integer.MIN_VALUE;
for (int i = 0; i < _hill.length; i++) {
hill[i] = Integer.parseInt(_hill[i]);
if(hill[i] > maxValue ) {
maxValue = hill[i];
}
}
int water = 0;
for (int i = 1; i <= maxValue; i++) {
List <Integer> barriers = new ArrayList<Integer>();
for (int j = 0; j < hill.length; j++) {
if(hill[j] >= i) {
barriers.add(j);
}
}
for (int j = 0; j < barriers.size() - 1; j++) {
water += barriers.get(j + 1) - barriers.get(j) - 1;
}
}
return water;
}
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
|
Java solution:
public class WaterInHill { public int[][] getHill(int[] x) { int max = 0;
for (int i = 0; i < x.length; i++)
{
if (x[i] > max)
{
max = x[i];
}
}
int[][] hill = new int[max+1][x.length];
for (int p = 0; p < x.length; p++)
{
for (int q = 0; q <= x[p]; q++)
{
hill[max - q][p] = 2;
}
}
return hill;
}
public int getWaterFilling(int[] x)
{
int[][] hill = getHill(x);
boolean[] filled = new boolean[x.length];
int sum = 0;
for (int row = 0; row < hill.length; row++)
{
for (int column = 0; column < hill[0].length; column++)
{
if (hill[row][column] == 2)
{
for (int p = column+1; p < hill[0].length; p++)
{
if (hill[row][p] == 2)
{
//set filled to true for all of them from row to p
//find the column height with respect to row
for (int i = column; i <= p; i++)
{
if (i > column && i <= p - 1 && filled[i] == false)
{
for (int q = row; q < hill.length && hill[q][i] == 0; q++)
{
sum++;
}
}
filled[i] = true;
}
}
}
}
}
}
return sum;
}
public static void main(String[] args)
{
WaterInHill obj = new WaterInHill();
int[] p = new int[]{4,2,4,1,5,3,16,6,17,19,4,13,5,3,10,10,13,6,2,1,5,15,13,19,16,9,13,1,7,18,20,13,9,7,2,10,8,18,4,7,5,8,10,13,7,18,19,2,19,8,10,10,17,6,6,20,20,11,10,11,13,9,7,1,10,5,12,16,10,7,15,13,12,10,1,1,4,2,16,10,20,17,11,19,19,20,9,10,17,9,18,8,10,18,8,19,16,17,3,1};
int water = obj.getWaterFilling(p);
System.out.println(water);
}
}
I have a nice algorithm but not the programming experience to implement it easily. I'm not sure if any of the programs proffered as solutions here use it.
-
Create a water counter initiate at W=0
-
Take the list of numbers and add a parallel list initially of all 1's.
-
Scan the original list and for any duplicate values, combine them and add together the corresponding values of the parallel list.
-
Scan the original list for any number smaller than its neighbor.
3a. Every time you find one, raise it to its lower neighbor. Multiply the amount raised by the value in the parallel list and add this to W. 3b. If the scan finds no number smaller than its neighbor display the value of W and end the program. -
Repeat steps 2 and 3 until you are done.
Here's an example with a shorter list
List: 10 1 2 7 3 9 5 4 6 8
Steps 0 & 1:
-
10 1 2 7 3 9 5 4 6 8 W = 0
-
1 1 1 1 1 1 1 1 1 1
Step 2 find no duplicates. Step 3
-
10 2 2 7 7 9 5 5 6 8 W = 0 + 1 + 4 + 1 = 6
-
1 1 1 1 1 1 1 1 1 1
Step 2
-
10 2 7 9 5 6 8 W = 6
-
1 2 2 1 2 1 1
Step 3
- 10 7 7 9 6 6 8 W = 6 + 5 ∗ 2 + 1 ∗ 2 = 1 8
- 1 2 2 1 2 1 1
Step 2
-
10 7 9 6 8 W=18
-
1 4 1 3 1
Step 3
-
10 9 9 8 8 W = 1 8 + 2 ∗ 4 + 2 ∗ 3 = 3 2
-
1 4 1 3 1
Step 2
- 10 9 8 W = 3 2
- 1 5 4
Step 3 finds no numbers in the original list smaller than its neighbor so the program ends and outputs W = 3 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
|
A significantly more compact solution than those I've seen here. The thought behind it is similar to Marta Reece's idea: Find the smaller one of the maximums of the subarrays to the left and right of the current position, subtract the current value from that, and if this gives a positive value, add it to a running total.
If, like me, you are on a crusade against the Zen of Python and think, "This returns one number, shouldn't it be one expression?", I've also provided an ultra-compressed version (yes, I sometimes code this way).
Both give the correct answer, 7 9 1 .
1 2 3 4 5 6 7 8 9 10 11 |
|
1 2 3 4 5 6 7 |
|
Here's a nice way to solve it in python using itertools and comprehensions, while being relatively efficient:
from itertools import accumulate
hills = [4, 2, 4, 1, 5, 3, 16, 6, 17, 19, 4, 13, 5, 3, 10, 10, 13, 6, 2, 1, 5, 15,
13, 19, 16, 9, 13, 1, 7, 18, 20, 13, 9, 7, 2, 10, 8, 18, 4, 7, 5, 8, 10, 13,
7, 18, 19, 2, 19, 8, 10, 10, 17, 6, 6, 20, 20, 11, 10, 11, 13, 9, 7, 1, 10,
5, 12, 16, 10, 7, 15, 13, 12, 10, 1, 1, 4, 2, 16, 10, 20, 17, 11, 19, 19, 20,
9, 10, 17, 9, 18, 8, 10, 18, 8, 19, 16, 17, 3, 1]
runningMax = list(accumulate(hills,max))
revRunningMax = list(reversed(list(accumulate(reversed(hills),max))))
filledHills = [min(x,y) for x,y in zip(runningMax, revRunningMax)]
water = [x-y for x,y in zip(filledHills, hills)]
print(sum(water))
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
|
Here’s the python code I used to solve the problem, I decided to go level by level and record the amount of empty spots that weren’t in the beginning or the ending spaces:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
|
I decided to get one of the tallest peaks, and work from wither end up until reaching said peak. This avoids having to worry about reaching the end of the list and accidentally overlooking any lower valleys.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
|
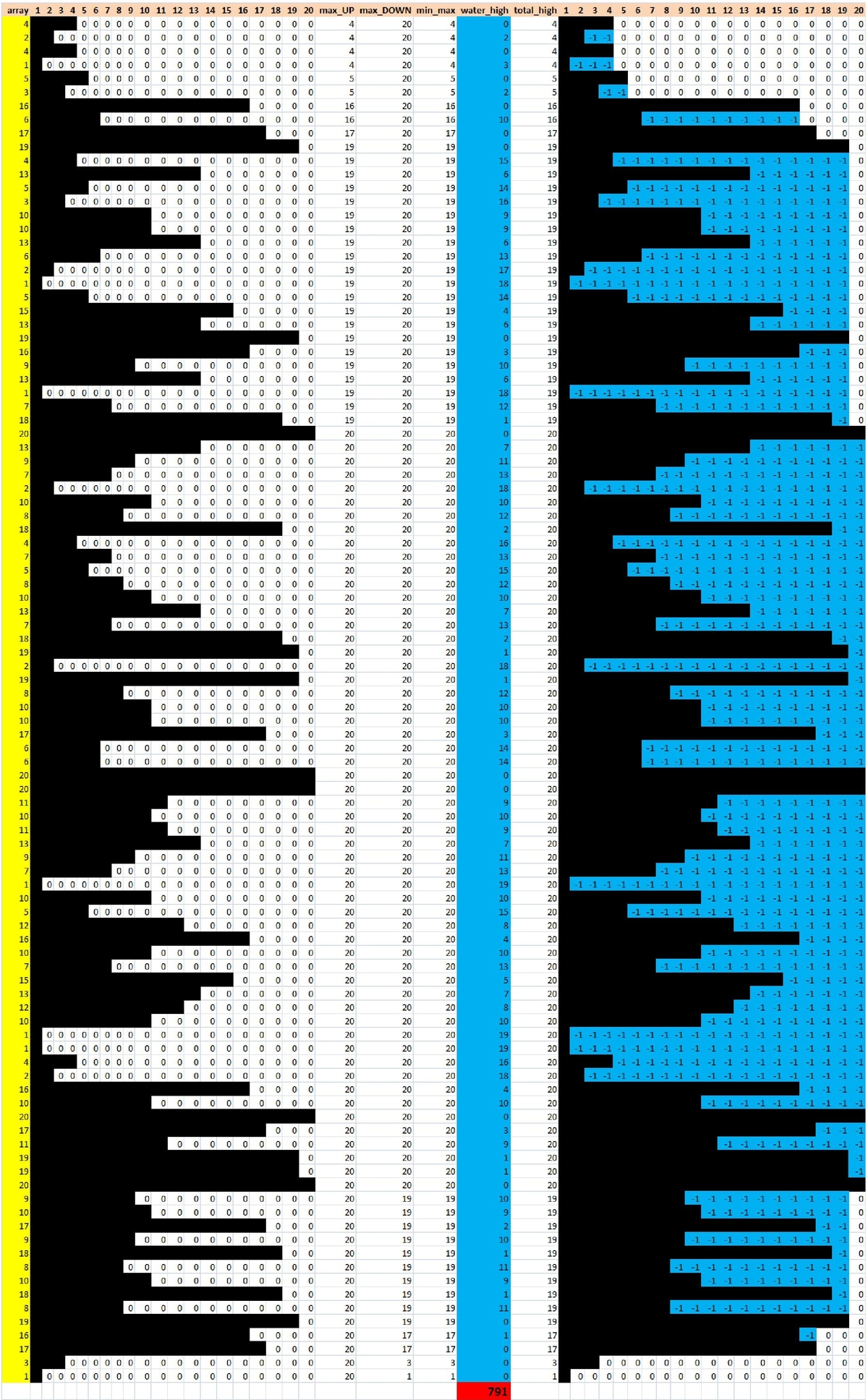
For each location calculate (1) the maximum of all the heights up to and including that point and (2) the maximum of heights from that point onward.
The smaller of those two numbers minus the height at that point is the water amount.
Add all the water amounts to get 7 9 1