Look out at the horizon

Classical Mechanics Level 3

At sunset, there is a moment at which the bottom of the Sun appears to touch the horizon. From this point on, the Sun dips further below the horizon until the point at which it finally disappears from view. How much time (in minutes) passes between the moment the Sun touches the horizon to the moment it disappears?

Details

  • The distance from the Earth to the Sun is 149.6 × 1 0 9 149.6\times10^9 m.
  • The radius of the Sun is 696.3 × 1 0 6 696.3\times 10^6 m
  • For simplicity, suppose that light always travels in straight lines and that you're standing at the Equator.

This problem was posed by the applied mathematician Vadim Patsalo


The answer is 2.13346.

Josh Silverman by Josh Silverman

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

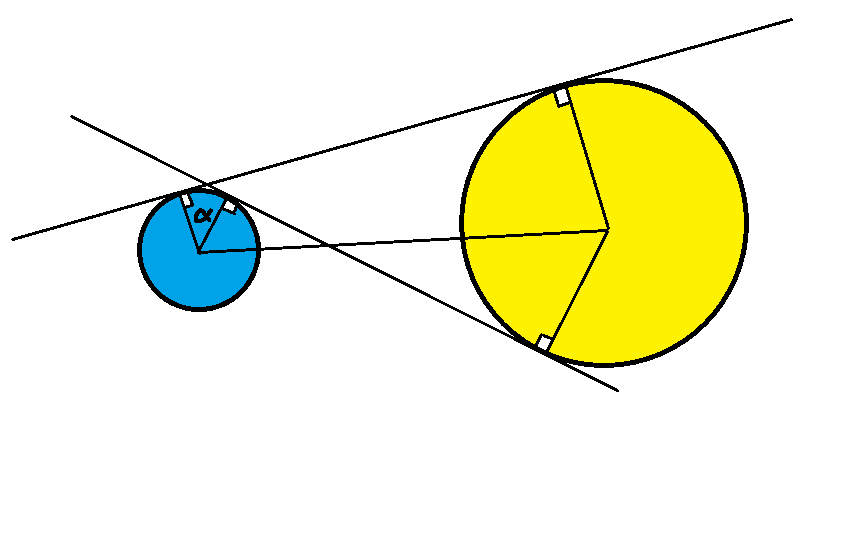Drawing (alpha is the key)

7 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

This is a superb illustration of the geometry of the problem.

Rimson Junio
Sep 1, 2015

Imagine a triangle whose sides are 149.6, 149.6, and 1.3926. Notice that the sides are scaled down and 1.3926 is the diameter of the sun. The angle opposite to 1.3926 is 0.533 4 ∘ 0.5334^{ \circ} . The sun traverses 36 0 ∘ 360^{\circ} in 24hours or 1440 minutes. So by proportion, x 0.533 4 ∘ = 1440 36 0 ∘ \frac{x}{0.5334^{ \circ}}=\frac{1440}{360^{\circ}} x = 2.1336 m i n x=2.1336 min

7 Helpful 0 Interesting 0 Brilliant 0 Confused

Can you elaborate more please ?

Especially the triangle ?

Syed Baqir - 5 years, 9 months ago

3 Helpful 0 Interesting 0 Brilliant 0 Confused

Nicely done.

Brilliant Physics Staff - 5 years, 9 months ago
Satvik Choudhary
Sep 1, 2015

Find the angle which diameter of sun subtend at earth. Find out what fraction of the total rotation of earth in a day it is then multiplying by 24 will give the answer in hours.

2 r / D = θ 2r/D = \theta θ 2 π × 24 × 60 = A n s \frac {\theta} {2 \pi} ×24×60 = Ans We are doing this to find out time in which earth rotates the angle which the sun subtends at any point on earth.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Slick. Would you have to modify this approach at all if the Sun were much closer to Earth?

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...