Waterloo University Problem-I

Algebra Level 2

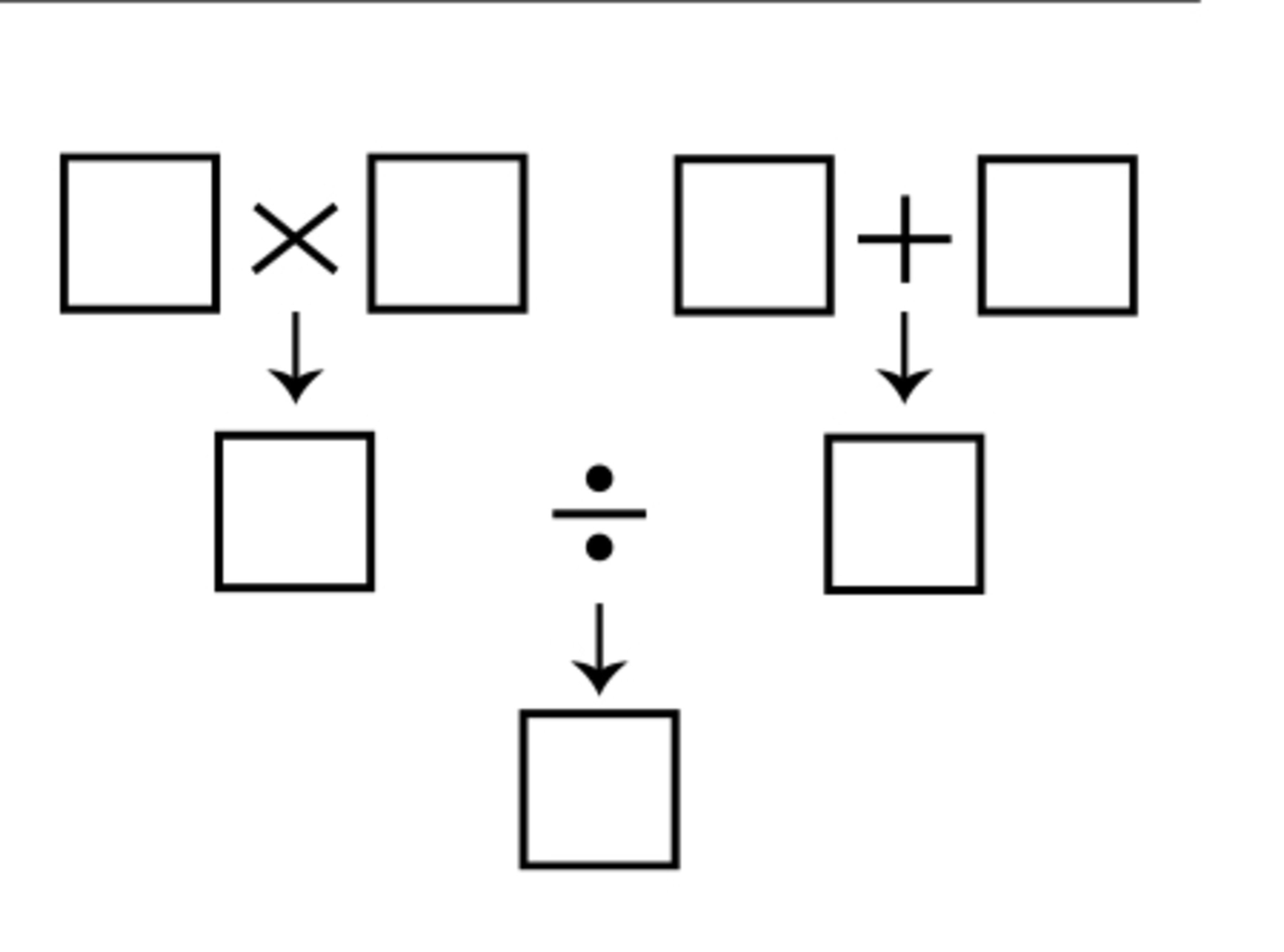
In the diagram, four different integers from 1 to 9 inclusive are placed in the four boxes in the top row. The integers in the left two boxes are multiplied and the integers in the right two boxes are added and these results are then divided, as shown. The final result is placed in the bottom box. Which of the following integers cannot appear in the bottom box?

20 24 7 16 9

Hana Wehbi by Hana Wehbi , 51, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

The minimum value for the right side is 3 (1+2), to get 20 the left side should be 60, but you can't multiply 2 integers smaller than 10 to get 60 (or larger multiples of 20).

3 Helpful 0 Interesting 0 Brilliant 0 Confused

For sake of completeness, we can obtain the other options as follows:

( ( 6 × 8 ) ÷ ( 1 + 2 ) = 16 , ( 9 × 8 ) ÷ ( 1 + 2 ) = 24 , ( 4 × 7 ) ÷ ( 1 + 3 ) = 7 , ( 7 × 9 ) ÷ ( 1 + 6 ) = 9 ((6 \times 8) \div (1 + 2) = 16, (9 \times 8) \div (1 + 2) = 24, (4 \times 7) \div (1 + 3) = 7, (7 \times 9) \div (1 + 6) = 9 .

The list of integers we can obtain includes 24 , 21 , 18 , 16 , 15 , 14 , 12 , 10 , 9 , 8 , 7 , 6 , 5 , 4 , 3 , 2 , 1 24, 21, 18, 16, 15, 14, 12, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 .

Brian Charlesworth - 2 years, 9 months ago

Thank you for sharing your solution.

Hana Wehbi - 2 years, 9 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...