Watermelon Riddle
An artist has delicately taken out a conical portion from a spherical watermelon with radius R = 5 , as shown.
Instead of a flat circular base, this special cone has a spherical cap (retaining its peel) with a cross-sectional base radius of r = 3 .
What is the ratio of the volume of the original whole sphere to that of this spherical cone?
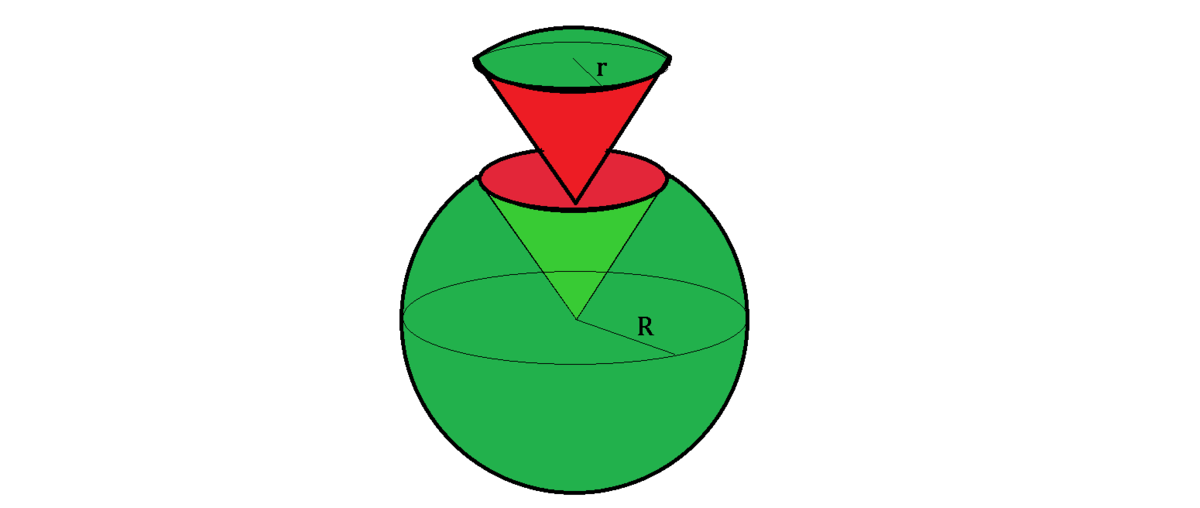
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Relevant wiki: Volume of a Sphere
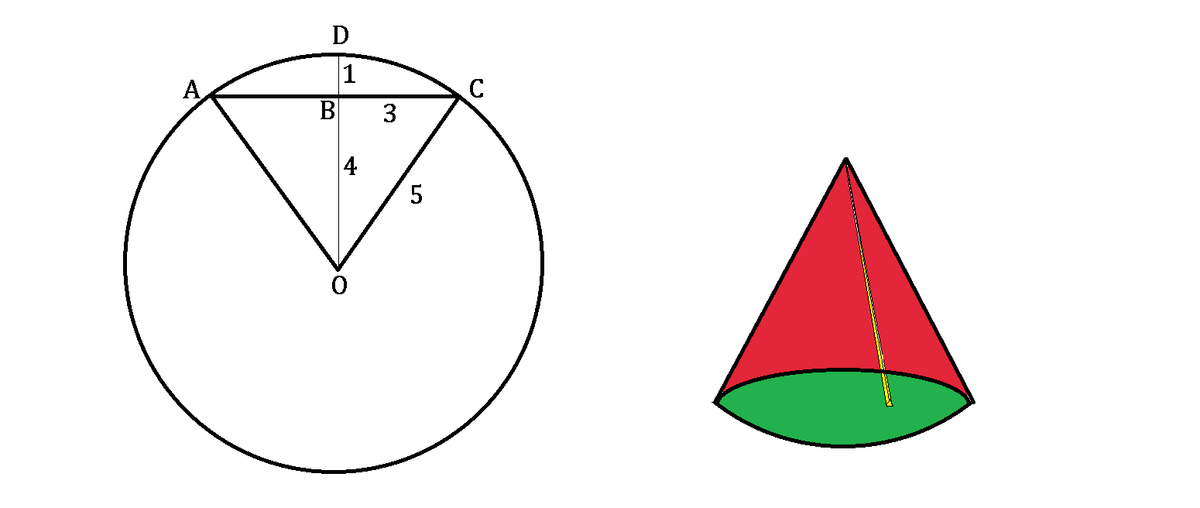
From the image above left, by Pythagorean theorem, we can calculate O B = R 2 − r 2 = 5 2 − 3 2 = 4 and so B D = R − 4 = 1 .
Then as shown in the image above right, the volume of this spherical cone can be divided into infinitesimal conic sub-units with height of R and base of d A . Each cone's volume = 3 1 ⋅ R ⋅ d A . Then by integration, we can obtain the whole volume, V :
V = ∫ 3 R d A
Since all cone sub-units have the same height R , we will get:
V = 3 R ⋅ A , where A is the surface area of the spherical cap.
Then by Archimedes' Hat-Box Theorem , the spherical cap area equals to the lateral surface area of the cylinder with the same radius R as the sphere and the same height as the cap, as shown below:
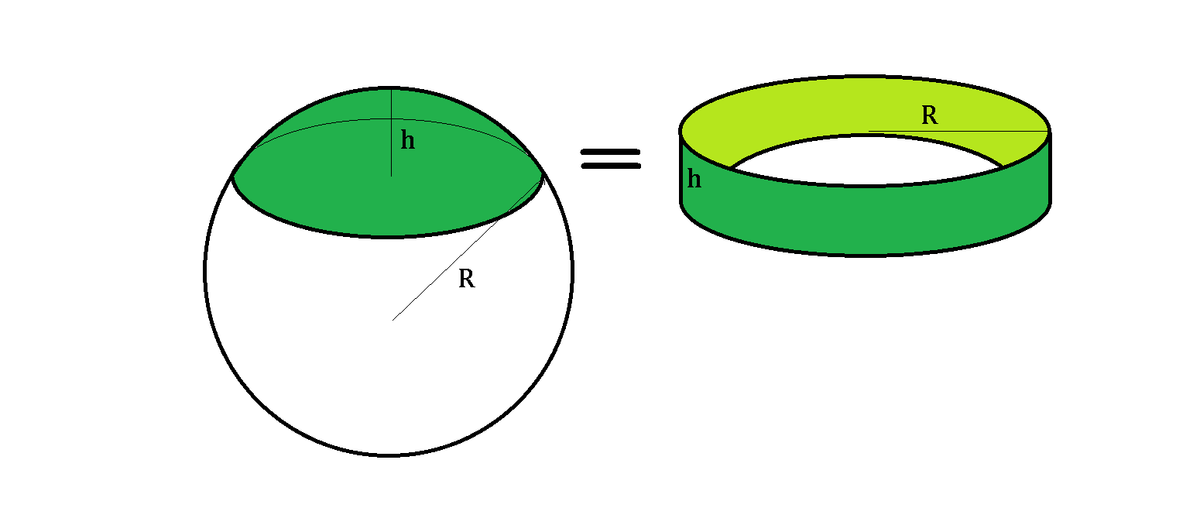
In other words, the surface area A of the spherical cap of height h = 2 π R h .
Plugging in the terms into the previous equation, we will get:
V = 3 R ⋅ A = 3 R ⋅ ( 2 π R h ) = 3 2 π R 2 h
As a matter of fact, if we plug in the surface area of the whole sphere for A , we will get:
V = 3 R ⋅ ( 4 π R 2 ) = 3 4 π R 3 , which is the formula for the sphere's volume.
Thus, the volume ratio of the sphere to the spherical cone is, in fact, the ratio of the surface area itself.
That is, the volume ratio = 3 2 π R 2 h 3 4 π R 3 = 3 R ⋅ ( 2 π R h ) 3 R ⋅ ( 4 π R 2 ) = h 2 R .
We know that R = 5 and h = B D = 1 . Therefore, the volume ratio = 1 2 ⋅ 5 = 1 0 .
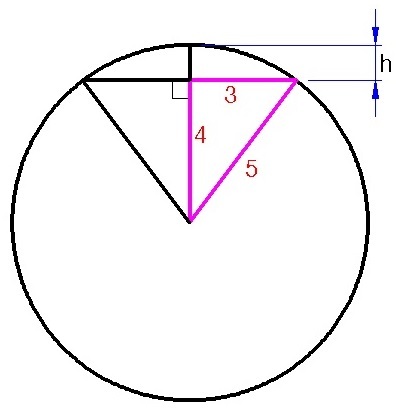 From the figure, we can see a
3
−
4
−
5
right triangle. So
h
=
5
−
4
=
1
. The volume of a spherical sector is given by
V
=
3
2
π
r
2
h
where
r
is the radius of the sphere and
h
is the altitude of its zone. Substitute:
V
=
3
2
π
(
5
2
)
(
1
)
=
3
5
0
π
. The volume of the whole sphere is
3
4
π
r
3
=
3
4
π
(
5
3
)
=
3
5
0
0
π
. In taking the ratio,
3
π
cancels out because it is present in the two volumes. So the required ratio is
5
0
5
0
0
=
1
0
A
N
S
W
E
R
From the figure, we can see a
3
−
4
−
5
right triangle. So
h
=
5
−
4
=
1
. The volume of a spherical sector is given by
V
=
3
2
π
r
2
h
where
r
is the radius of the sphere and
h
is the altitude of its zone. Substitute:
V
=
3
2
π
(
5
2
)
(
1
)
=
3
5
0
π
. The volume of the whole sphere is
3
4
π
r
3
=
3
4
π
(
5
3
)
=
3
5
0
0
π
. In taking the ratio,
3
π
cancels out because it is present in the two volumes. So the required ratio is
5
0
5
0
0
=
1
0
A
N
S
W
E
R
V s s = 3 2 π R 2 h , where: R =radius of the sphere and h = height of the segment
Substituting, we get
V s s = 3 2 π ( 5 2 ) ( 1 ) = 3 5 0 π
Solving for the volume of the original sphere, we have
V = 3 4 π R 3 = 3 4 π ( 5 3 ) = 3 5 0 0 π
Finally, the volume ratio of the original sphere to the spherical cone is
ratio of volume = 3 5 0 π 3 5 0 0 π = 5 0 5 0 0 = 1 0 answer