Number of Pathways
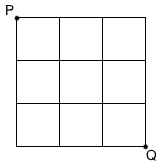 How many distinct paths consisting of steps only right or down are possible from
to
?
How many distinct paths consisting of steps only right or down are possible from
to
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Solution:
Here we see that by travelling through any way, we have to take 3 horizontal and 3 vertical steps. So no of ways of arranging hhhvvv = (6!/3!3!) = 20 ways