You're Only Getting Cake Because My Mum Forced Me To Give It To You

Greedy Garisht is celebrating his birthday with 6 of his friends. His mother baked him a birthday cake in the shape of a regular hexagon. Wanting to keep most of the cake, he makes cuts linking the midpoints of every 2 adjacent sides, and distributes these 6 slices to his friends. What proportion of the cake does he have left for himself?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Yeah Same here man . :)
Olm yeter laaaan. I WANT TURKISH LANGUAGE SUPPORT. IF YOU DONT CHANGE İMMEDİATELY, I WİLL SPREAD BAD GOSSİP ABOUT THİS APPLICIATION. AYAÑIZI DEÑG ALIÑ!!!
WLOG let sidelength of the hexagon equal 1 , then note that joining the midpoints will make hexagon that is regular because for each side length a of this new hexagon we get by the law of cosines:
a 2 = ( 2 1 ) 2 + ( 2 1 ) 2 − 2 ⋅ 2 1 ⋅ 2 1 ⋅ cos ( 3 2 π ) = 4 3 and the ratio of areas is 1 2 a 2 = 4 3 .
Here is an equally effective solution:
Circumscribe circles around the two hexagons. We will compare the areas of these circles instead, since similarity preserves ratios. Let the radius of the larger circle be 2 ; then, the radius of the smaller circle is obviously 3 by the 30-60-90 triangle, and the ratio of their areas is ( 2 3 ) 2 = 4 3 .
Nice work!
Please can anyone explain me a bit about law of cosines and sines
Using Trig and the fact that the interior angles of a regular hexagon with side s are 1 2 0 ∘ . We find that the area of a single piece of cake is 1 6 s 2 3 hence the sum of the areas of all the pieces is 8 s 2 3 3 . Again,using trig ,we can derive the area of a regular hexagon to be 2 s 2 3 3 . The ratio of the two formulae gives 2 s 2 3 3 1 6 s 2 3 = 4 1 . This is the ratio of slices of cake to total cake and we subtract this ratio from 1 to get the remainder of the cake. 1 − 4 1 = 4 3
same method
The area of the cake is proportional to s 2 where s is the length of the side hexagon. We can write this as A = k s 2 , k being the proportionality constant. The resulting shape, right after Greedy Garisht sliced his cake, is also a regular hexagon with area defined by A n e w = k ( s n e w ) 2 . To obtain the ratio s n e w : s , we consider one of the sliced portion he gave to his friends. It is shaped as an isosceles triangle, with vertex angle equal to 1 2 0 o and leg length equal to 2 s } . One can verify that the base length is equal to { 2 3 s } by using either cosine law or dividing the triangle into two 3 0 o − 6 0 o − 9 0 o right triangles and use sine law to obtain half of the base length. The base length is also equal to the side length of the new hexagon, thus we have: A n e w = k ( 2 3 s ) 2 = 4 3 k s 2 = 4 3 A . Thereby the proportion of the cake left to himself is: A A n e w = 4 3 .
3/4
Non-trig and easy-to-understand solution:

We get another hexagon by cutting midpoints of the adjecent sides.
If side of hexagonal cake is a, then side of this hexagon becoms ((a/2)^2+(a/2)^2-2(a/2)(a/2)cos(120))^(1/2)=(3^(1/2))a/2
Now, area is proportional to (side)^2
So, fraction is equal to 3/4
Let the side of the hexagon be x .
Area of a regular polygon equals 4 t a n ( N 1 8 0 ) S 2 N
A h e x a g o n = 4 t a n ( 6 1 8 0 ) x 2 × 6
which simplifies to 2 3 9 x 2
The some of interior angles in a regular polygon is given by 1 8 0 ( n − 2 )
And this equals 1 8 0 ( 6 − 2 )
and 7 2 0
Thus each interior angle of the hexagon equals 120
With the manner in which he divided the cake, he created 6 isosceles triangles of sides x/2 around the hexagon .
Area of the isosceles triangles equals 6 × 2 1 × 2 x × 2 x × s i n 1 2 0
And this simplifies to 1 6 x 2 3
Expressing this area as a fraction of the entire area of the hexagon we get 8 3 x 2 3 × 9 x 2 2 3
which simplifies to 4 1
Thus the proportion of cake that he has left to himself equals 1 − 4 1
Which gives 4 3
when Garisht is done with giving slices to his firneds, the hexagonal cake becomes a smaller hexagon. the side of new hexagon is \sqrt{3} /2 times the legth of side of the old hexagon. The area of new hexagon will be 3/4 times of that of old hexagon
56
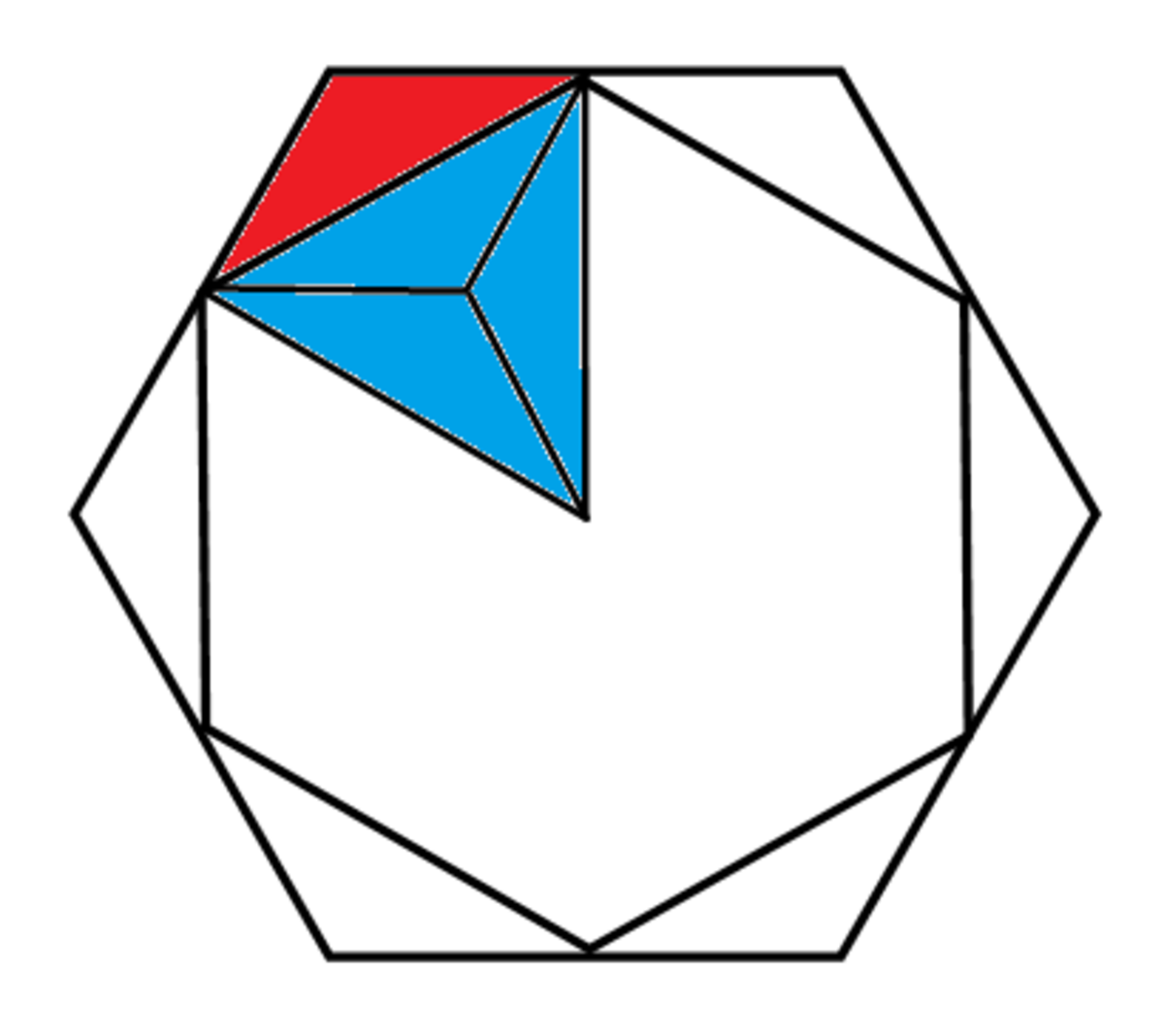
Area of regular hexagon with side length s is: A = 2 3 3 s 2
Note: Internal angles of a regular hexagon are 1 2 0 ∘ .
Using this we can derive the area A s of each section cut: A s = 1 6 3 s 2
Total area of the sections cut is: 6 A s = 8 3 3 s 2
Ratio between the sections cut and the rest of the cake is: A 6 A s = 2 3 3 s 2 8 3 3 s 2 = 4 1
This means the proportion that Garisht keeps is 4 3