We are all made of stars
Consider a five-pointed star made of resistors as shown below. Each resistor has resistance
R
=
6
Ω
. Find the equivalent resistance
in Ohms
between the points A and B.
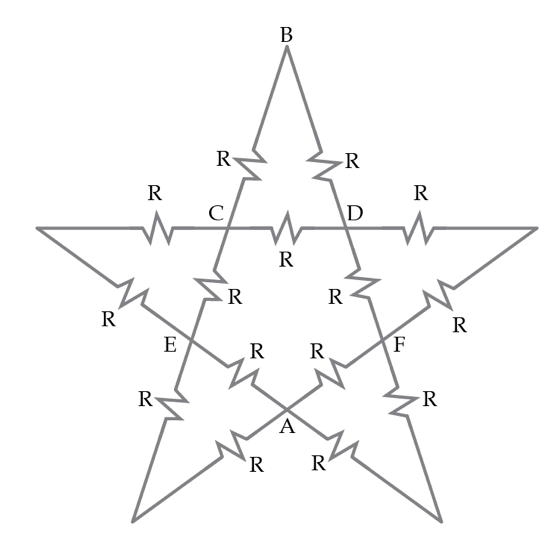
Details and assumptions
Note: Points ABCDE are labeled for easy reference if you need to use some combination of them in a solution.
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Discussions for this problem are now closed
how come you can't get your 4 ohms on all 5 points then add them together to get 20 ohms?
it's easier to work it out from point B to point A
from point B we can see that the current is split into two part, to point C and point D.
point C to E is a parallel circuit, as well as point E to A
point D to F and F to A is identical with point C to E and E to A so we can use the same method to calculate them.
there's no current flowing through the resistor in between C-D, so we don't have to calculate that.
calculating the resistor value:
point A-E = E-C = A- F= F-D
1/6+1/12 = 1/R
R= 4 ohms
point A-C = A-D
R= 4+4 = 8 ohms
parallel circuit A-B
1/14 +1/14=1/R
Rsum= 7 ohms
Between points ( A , E ), ( E, C ), ( A , F ) and ( F , D ) two resistors in series are parallel withanother resistor.
\Rightarrow net resistance between A and E
= ( R + R ) + R ( R + R ) ⋅ R
( this is because net resistance in parallel = R 1 + R 2 R 1 ⋅ R 2 )
= 3 2 R
Similarly, net resistance between ( E, C ), ( A , F ) and ( F , D ) = 3 2 R so, total resistance between A and C & A and D = 3 4
Now, redrawing the diagram and a close look will reveal the formation of 'Weatsone-bridge'.
Hence no current flows in wire C D . Therefore, resistance in branch \overline{AC} is in series with C B . So, net resistance in \overline{ACB} is 3 4 R + R = 3 7 R .
the net resistance between A and B is 6 7 R = 7 Ω .
due to junction separation at c nd d the equivalent resistance is 4R/3 THEN apply whestone bridge at junction abcd so that cd connection is removed then ac nd cb are in series similarly ad nd bd r in series so that the ev resistance is 7R/3 THEN the two r in parallal so answer is 7R/6=7
The "outer" resistors along CE, EA, AF, and FD have a total resistance of 12 ohms. In parallel with each 6-ohm resistor along the pentagon, the equivalent resistance between each of the four pairs is 4 ohms. AC and AD then have equivalent resistances of 8 ohms (2 four-ohm resistors in series). ACD can then undergo a delta-wye transformation. This results in the 8-8-4 delta being equivalent to a 3.2-1.6-1.6 wye. Each 1.6-ohm resistor is then in series with a 6-ohm resistor (either BC or BD). The parallel pair of 7.6-ohm resistors is then equivalent to 3.8 ohms. Combined in series with the last 3.2-ohm resistor from the delta-wye transformation yields the final result of 7 ohms.
Hint : Break the star into simple circuits
Resistance between D & F consisting of 3 resistance in which two are in series and one in parallel with the other two = (2/3) R Similarly resistance between F& A, A &E, E & C are also the same i.e (2/3) R
This means resistance between CE = resistance between EA =resistance between AF =resistance between FD = (2/3) R
Now resistance between CA = resistance between AD = (4/3) R
Now the star has reduced into a balanced Wheatstone Bridge. Thus no current will flow through the wire CD, hence the wire could be removed.
Resistance in wire AFDB = Resistance in wire AECB = (7/3) R
Hence net resistance between A & B = (1/2) * (7/3) R = (7/6) R Substituting value of R = 6ohm we get net resistance between A & B as 7ohm
Note that the resistances between C and E, D and F, F and A, and E and A are a simple section of two parallel branches, with one having two of the resistors in series and the other having one resistor. Thus the total resistance between the mentioned nodes becomes 4 ohms.
Next, the path from C to A and the path from D to A becomes a series circuit with two 4-ohm resistors. The total resistance along these paths is 8 ohms.
We now arrive at a unbalanced Wheastone bridge-like configuration, with the top 3 resistors in a triangle with side lengths 6 ohms and the bottom two parts of the unbalanced bridge being of 8 ohms. Applying a delta-wye transformation to the top three resistors, we find that the resistance of each of the resistors in the wye configuration is 2 ohms.
Now, the resistors between B and A have a 2 ohm resistor connected in series with a parallel network, whose branches each have resistance 10 ohms. Thus the total resistance of the parallel part is 5 ohms, and in series with the 2 ohm resistor we arrive at the fact that the resistance between B and A is 7 ohms.
Not a solution, but a hint!! After you get to the point where you can see a triangle ADC of resistances, Use WHEATSTONE'S METER BRIDGE CONCEPT to (i) either rule out the resistance between C & D or (ii) Short circuit the points C & D. Then carry on with your simple calculations!!
can star delta conversions not be used??????
You should use it only when there's no other way out!!!
ya we have to use at point B only
A somewhat simple minded approach seems to be to enumerate all paths from B to A and treat each path as composed of a series of resistors and then treat each path in parallel with other paths. A more systematic approach seems to be to use concepts such as spanning tree etc as well as Kirchoff's laws etc
The problem seems to become simpler if we consider that if we traverse an edge say CD in 1 direction, if we traverse in the reverse direction, one may have to multiply by -1
Evaluating the equivalent resistance of one side of the star's pentagon (AECDFA), we get 6 1 + 1 2 1 = S i d e 1 ⇒ A E = A F = E C = F D = 4 Ω .
Because A C = A E + E C and A D = A F + F D , we get A C = A D = 8 Ω .
We now are left with a square-like circuit ACBDA, with a connection between C and D. This connection's resistance can be despised because no electric current goes through it (Wheatstone Bridge). Because A B = A C + C B = A D + D B , we finally get 8 + 6 1 + 8 + 6 1 = F i n a l 1 ⇒ F i n a l = 7 Ω .