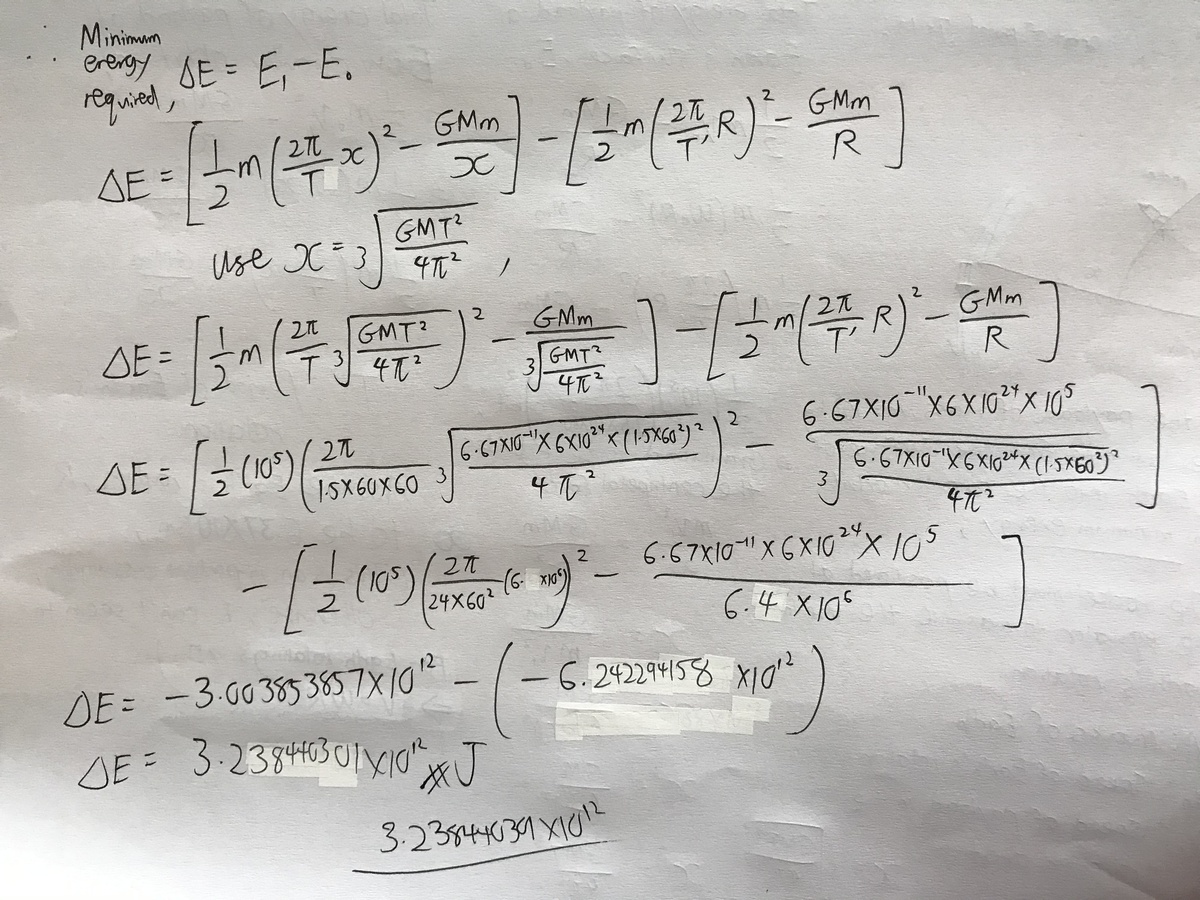We have liftoff, but we don't want to fall back to earth

Once we have liftoff, we obviously can't just turn off the engines as the rocket would fall back to earth. It takes a lot of energy to get a rocket into orbit, and so there is a lot of work that needs to be done on the rocket by the exploding fuel to get it into orbit. What is the minimum energy in Joules does it take to get a payload of $10^5$ kg from the surface of the earth into a circular orbit of period 1.5 hours?

The mass of the earth is $6 \times 10^{24}$ kg. $G_N=6.67 \times 10^{-11}~N m^2/kg^2$ .

Neglect complicating factors like air resistance.