We play! The game of the five balls and the three openings
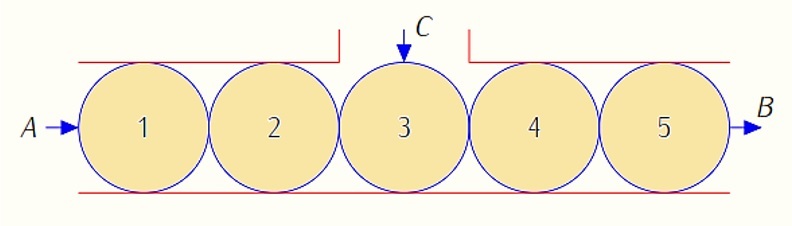
For a game a tube containing five balls numbered from 1 to 5 is used. It has three openings A and B at the ends and C in the middle at the top, as shown.
Game rules:
1) You can take a ball through the opening B and enter it by A, moving the other balls to the right.
2) You can take a ball through the opening B and enter it by C, moving the last two balls to the right.
If initially the balls are in position 12345, what is the minimum number of moves needed to reach position 25413?
Example: Suppose that at some point the balls are in position 14352 there are two possible moves:
- Take the 2 ball by B and enter it by A, remaining as new position 21435.
- Take the 2 ball by B and enter it by C, remaining as new position 14235.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
How can we justify that 5 is indeed the minimum no of steps needed??
Log in to reply
If we look at the final required position, it is obvious that the last ball to be moved is either 2 or 4. However, balls are only removed at B. Therefore the first ball moved is definitely 5, followed by a 4. It is obvious that the 2 must be moved to the front, so at least 4 moves are needed (5,4,3,2) to move it to the front. For it to be done in 4 moves, the 5 ball must be moved to A (as placing it at C would shunt the 2 ball further down the line). However, this creates a '51' combo, which isn't in the required end position. Going round to get rid of it would take more than 4 moves. Therefore, the lower bound is 5.
Possible positions at every step are:-
(i) 5 1 2 3 4 , 1 2 5 3 4
(ii) 4 5 1 2 3 , 5 1 4 2 3 , 4 1 2 5 3 , 1 2 4 5 3
(iii) 3 4 5 1 2 , 4 5 3 1 2 , 3 5 1 4 2 , 5 1 3 4 2 , 3 4 1 2 5 , 4 1 3 2 5 , 3 1 2 4 5 , 1 2 3 4 5
(iv) 2 3 4 5 1 , 3 4 2 1 5 , 2 4 5 3 1 , 4 5 2 3 1 , 2 3 5 1 4 , 3 5 2 1 4 , 2 5 1 3 4 , 5 1 2 3 4 , 5 3 4 1 2 , 3 4 5 1 2 , 5 4 1 3 2 , 4 1 5 3 2 , 5 3 1 2 4 , 3 1 5 2 4 , 5 1 2 3 4 , 1 2 5 3 4
(v) 1 2 3 4 5 , 2 3 1 4 5 , 5 3 4 2 1 , 3 4 5 2 1 , 1 2 4 5 3 , 2 4 1 5 3 , 1 4 5 2 3 , 4 5 1 2 3 , 4 2 3 5 1 , 2 3 4 1 5 , 4 3 5 2 1 , 3 5 4 2 1 , 4 2 5 1 3 , 25413 , 4 5 1 2 3 , 5 1 4 2 3 , 2 5 3 4 1 , 5 3 2 1 4 , 2 3 4 5 1 , 3 4 2 5 1 , 25413 , 5 4 2 1 3 , 2 4 1 5 3 , 4 1 2 5 3 , 4 5 3 1 2 , 5 3 4 1 2 , 4 3 1 5 2 , 3 1 4 5 2 , 4 5 1 2 3 , 5 1 4 2 3 , 4 1 2 5 3 , 1 2 4 5 3
One such solution:
12345
12534
41253
41325
54132
25413