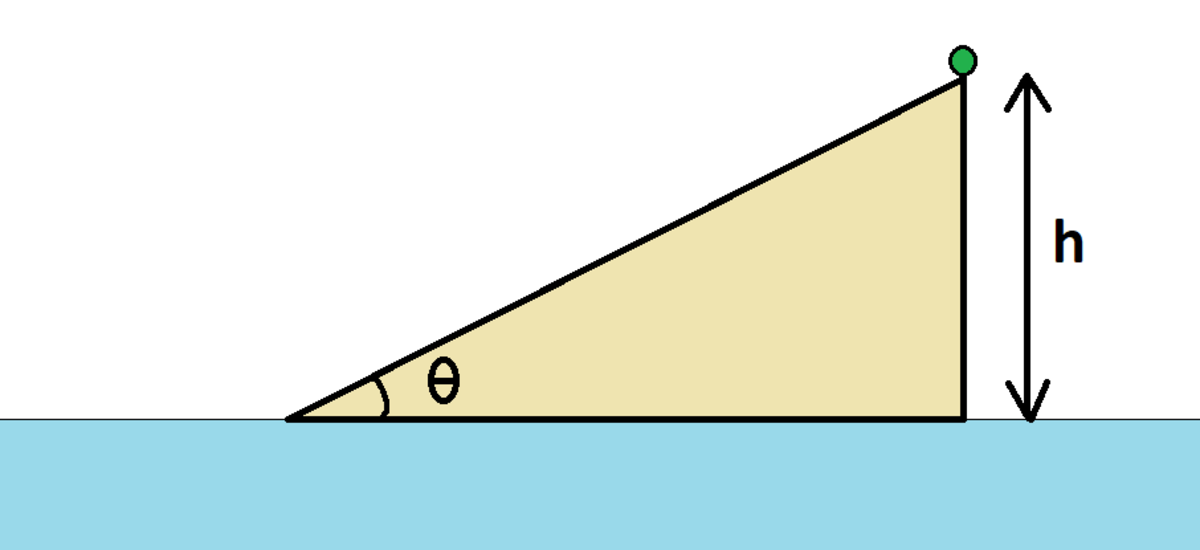
Wedge and Block

Classical Mechanics Level 3

A triangular wedge has height h h and mass M M , and it makes an angle θ \theta with the horizontal. The wedge sits on a smooth horizontal surface, and can slide freely on the surface. The ambient gravitational acceleration g g is downward.

There is a block of mass m m on the slanted part of the wedge, where it can slide freely. Initially, both the block and the wedge are at rest, and the block is at the top of the wedge.

When the block gets to the bottom of the wedge, how fast is the wedge moving?

Inspiration

Details and Assumptions:
1) The block has reached the bottom of the wedge, but has not left the wedge
2) h = 10 h = 10
3) M = 1 M = 1
4) θ = π / 6 \theta = \pi/6
5) m = 1 m = 1
6) g = 10 g = 10


The answer is 7.746.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Acceleration of the wedge is w 2 = m g sin ⁡ θ cos ⁡ θ M + m sin ⁡ 2 θ = 2 3 w_2=\dfrac {mg\sin \theta \cos \theta }{M+m\sin^2 \theta }=2\sqrt 3 m/s 2 ^2

Acceleration of the block relative to the wedge is w 1 = ( m + M ) g sin ⁡ θ M + m sin ⁡ θ = 8 w_1=\dfrac {(m+M)g\sin \theta }{M+m\sin \theta }=8 m/s 2 ^2

Distance covered by the block relative to the wedge is s = h cosec ⁡ θ = 20 s=h\cosec \theta =20 m.

Hence time to cover this distance is t = 2 s w 1 = 5 t=\sqrt {\dfrac {2s}{w_1}}=\sqrt 5 sec.

Therefore the velocity of the wedge at this time is v 2 = w 2 t = 2 3 × 5 = 2 15 ≈ 7.7459666 v_2=w_2t=2\sqrt 3\times \sqrt 5=2\sqrt {15}\approx \boxed {7.7459666} m/s.

1 Helpful 1 Interesting 2 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...