Wedge Hedge
From the diagram below, a block of mass lies on the surface of mass . The wedge is connected to another mass hanging over a pulley of mass . What must be the hanging mass such that the smaller mass on the wedge does not slip up or down relative to the wedge?
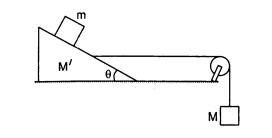
Assumptions:
- All surfaces are frictionless
- Pulleys and rope are weightless
- g =
- Force of tension is the same throughout the whole rope.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1) The horizontal accelerations of M ′ and m are equal, and are the same as the vertical acceleration of M
2) The vertical acceleration of m is zero
Let T be the rope tension and N be the magnitude of the normal reaction force between m and the ramp. Translating into math yields:
M M g − T = M ′ T − N s i n θ = m N s i n θ N c o s θ = m g
Substituting in for the normal force magnitude gives:
M M g − T = g t a n θ M ′ T − m g t a n θ = g t a n θ
Further substitution:
M ( g − g t a n θ ) = T = M ′ g t a n θ + m g t a n θ M = g − g t a n θ M ′ g t a n θ + m g t a n θ = c o t θ − 1 M ′ + m