Wedges in a triangle 1

Label the points as shown below, and draw $EF$ as the bisector of the sector and also draw $BC$ .

Since $\triangle ABC$ is a unit equilateral triangle, $BC = 1$ , and since $DE = BC$ , $DE = 1$ .

As a radius of the sector, $EF = 1$ , and as a bisector of the $60°$ angle, $\angle FEG = 30°$ , and as a tangent, $\angle EFG$ is a right angle. Therefore $EG = \frac{1}{\cos 30°} = \frac{2}{\sqrt{3}}$ .

The side length $DG$ is therefore $DE + EG = 1 + \frac{2}{\sqrt{3}}$ , so $A = 1$ , $B = 2$ , and $C = 3$ , and $A + B + C = \boxed{6}$ .

The exact side length is $1+\frac{2}{\sqrt{3}}$ so the answer is $1+2+3=\boxed{6}$ .

The y-coordinates of the 3 apexes are 0, 1 and cos 60°. Their mean must be the center of the triangle, $\frac{1+\frac{1}{2}\sqrt{3}}{3}$ , so the height of the triangle is 3 times this $h=1+\frac{1}{2}\sqrt{3}$ , and the side $s=\frac{2h}{\sqrt{3}}=\frac{2}{\sqrt{3}}+1$ , so the answer is 1+2+3=6

Since i think noone has managed to over-complicate things as much as i usually do, here's how i solved this:

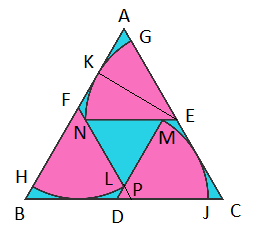
Since EGN is a sector of a unit circle, EK = 1, and since $\angle NEG = 60^\circ$ then $\angle AEK = 30^\circ$ , and AE = 2 * AK. Using Pythagoras, $3\times AK^2 = EK^2 = 1$ so $AK=\frac{1}{\sqrt3}$ . Since AE = 2 * AK, $AE =\frac{2}{\sqrt3}$ .

Due to symmetry, $BF = CD = AE =\frac{2}{\sqrt3}$ . And $CJ = CD - DJ = \frac{2}{\sqrt3} -1$ .

Extending FL until it meets BC at P, we have $\angle LDP = \angle MDJ = 60^\circ$ . Since ABC is equilateral, then $\angle ABC = 60^\circ$ , and since $\angle BFP = \angle HFL = 60^\circ$ then $\angle FPB = \angle LPD = 60^\circ$ , therefore the LPD triangle is also equilateral.

Thus $BC = BP + CD - DP = BF + CD - (FP - FL) = \frac{2}{\sqrt3} + \frac{2}{\sqrt3} - (\frac{2}{\sqrt3} - 1) = 1 + \frac{2}{\sqrt3}$ . So $A=1, B=2, C=3$ , and $A + B + C = \boxed{6}$ .