Wedges in a triangle 2
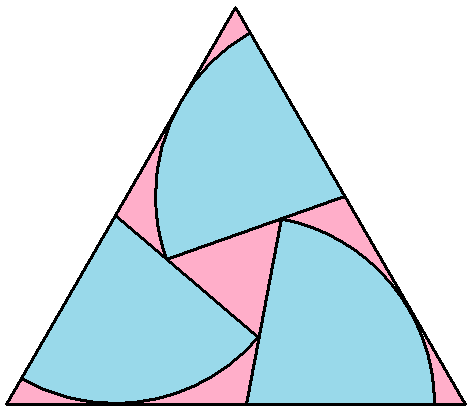
Three congruent sectors of a circle fit tightly inside an equilateral triangle as shown. The angle of the sectors is between and .
Find the maximum proportion of the triangle filled by the sectors.
The answer is 0.8156886563.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If there's a closed form I don't plan find it. See the complicated function to be maximized below. The maximum occurs when the angle is about 7 9 . 7 3 7 9 1 9 7 7 ∘
Let the sectors have unit radius then the total area of the sectors is A ( θ ) = 3 ⋅ θ ⋅ 3 6 0 ∘ π where θ is the angle in degrees.
The formula for the side length is S ( θ ) = 2 sin θ 2 3 sin θ − 2 cos θ + 3
The proportion to be maximized is then P ( θ ) = 4 3 S 2 A
Which I first maximized with Geometer's Sketchpad and then confirmed with my graphing calculator which gives more digits of accuracy.