Weighted summing amplifier
Consider the following circuit.
R
1
=
1
Ω
,
R
2
=
2
Ω
,
R
3
=
3
Ω
, and
R
4
=
4
Ω
.
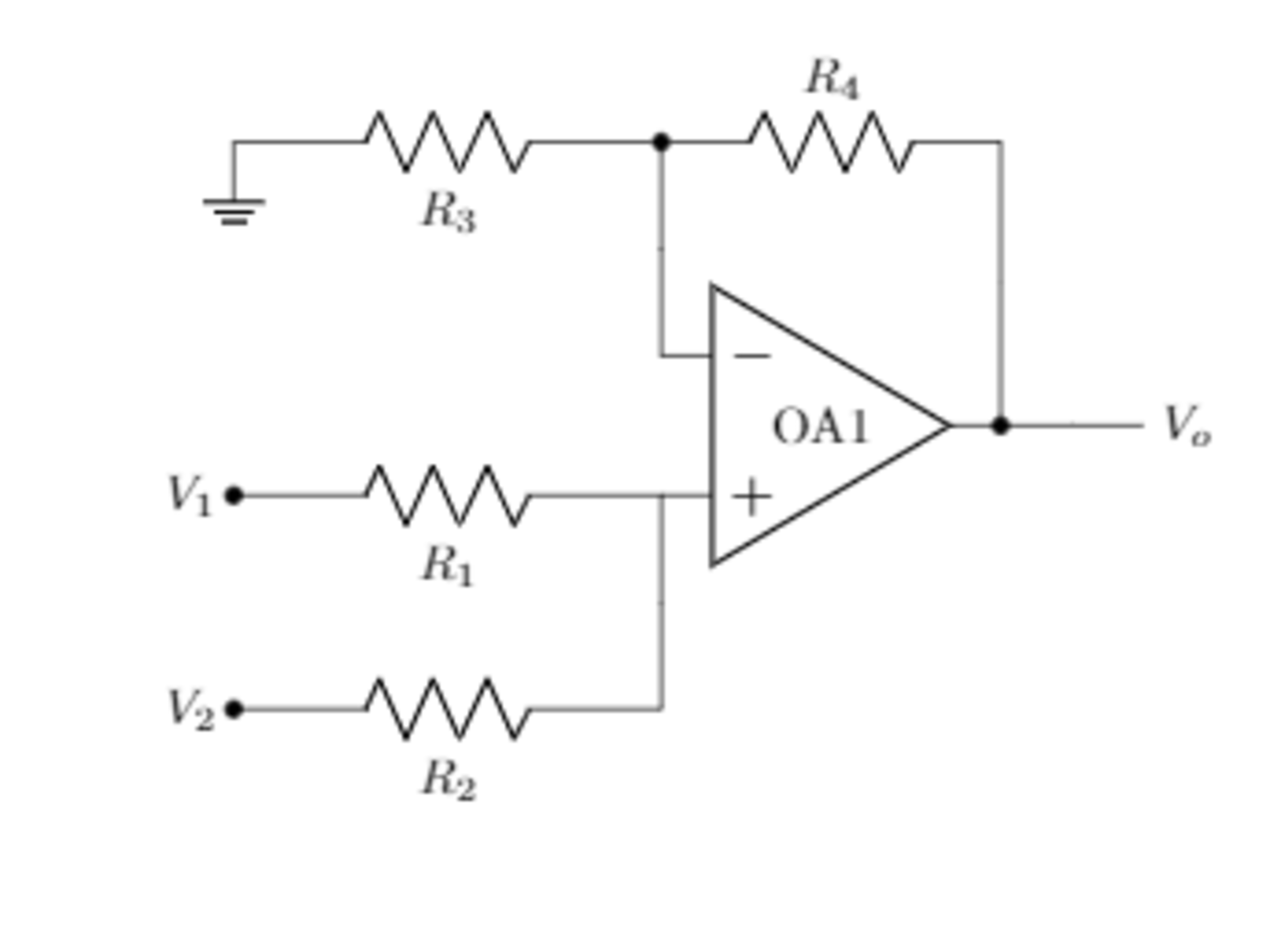 The output voltage can be expressed as
V
o
=
x
V
1
+
y
V
2
. If
x
+
y
=
b
a
where
a
and
b
are positive co-prime integers, enter
a
+
b
.
The output voltage can be expressed as
V
o
=
x
V
1
+
y
V
2
. If
x
+
y
=
b
a
where
a
and
b
are positive co-prime integers, enter
a
+
b
.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution, Charley! At Purdue's ECE program, we teach our Sophomores the wonderful "Op-Amp Chant"........Oppie the Amp loves his matching voltages (V+ = V-), but ain't got time for current drama (I+ = I- = 0)! Well, at least it still works for me 25 years later :)
Considering that OPAMP input currents are 0 , we can calculate the voltage at the "+" input using superposition:
V + = R 1 + R 2 R 2 V 1 + R 1 + R 2 R 1 V 2 = 3 2 V 1 + 3 1 V 2
The "+" input sees the rest of the circuit as a non-inverting OPAMP configuration, so we can write:
V o = ( 1 + R 3 R 4 ) V + = 3 7 ( 3 2 V 1 + 3 1 V 2 ) = 9 1 4 V 1 + 9 7 V 2
i 1 = R 1 + R 2 V 1 − V 2 V + = V − = V 1 − i 1 R 1 = V 1 − R 1 + R 2 ( V 1 − V 2 ) R 1 i 2 = R 3 V − V o = i 2 ( R 3 + R 4 ) = R 3 V − ( R 3 + R 4 ) = ( V 1 − R 1 + R 2 ( V 1 − V 2 ) R 1 ) R 3 R 3 + R 4 V 0 = ( R 1 + R 2 V 1 ( R 1 + R 2 ) − V 1 R 1 + V 2 R 1 ) ( R 3 R 3 + R 4 ) V o = ( V 1 R 2 + V 2 R 1 ) ( R 3 ( R 1 + R 2 ) R 3 + R 4 ) V o = x ( R 3 ( R 1 + R 2 ) R 2 ( R 3 + R 4 ) ) V 1 + y ( R 3 ( R 1 + R 2 ) R 1 ( R 3 + R 4 ) ) V 2
x = 3 ( 1 + 2 ) 2 ( 3 + 4 ) = 9 1 4 y = 3 ( 1 + 2 ) 1 ( 3 + 4 ) = 9 7 x + y = 3 ( 1 + 2 ) 2 ( 3 + 4 ) = 9 1 4 + 9 7 = 9 2 1 = 3 7 Therefore, a = 7 and b = 3 so a + b = 1 0 .