Weird Continuity
How many of the following functions are continuous for all ?
Notation: denotes the floor function, denotes the fractional part function.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A continuous function is 'connected': for any point the limit as we approach from the positive side, the limit as we approach from the negative side, AND the point itself must all have the same value.
Both the floor function and the fractional part function are continuous for non-integer values of x and discontinuous for integers, and their value when approaching an integer from the positive side is the same as the value of the function at that point, but different to the value of the function when approached from the negative side.
Let us consider an integer k . When we approach ⌊ k ⌋ from the positive side, we get k , but when we approach from the negative side, we get k − 1 , as we are taking the floor of numbers slightly smaller than k. When we approach { k } from the positive side, we get 0 as the fractional part is decreasing, but when we approach from the negative side, we get 1 as the fractional part is increasing.
But what if we add these two functions together, and take the limit of ⌊ x ⌋ + { x } from both sides? x → k + lim ⌊ x ⌋ + { x } = ( k ) + ( 0 ) = k x → k − lim ⌊ x ⌋ + { x } = ( k − 1 ) + ( 1 ) = k We get the same result for each limit, and since the value of the function as we approach a point from the positive is the same as the value of the function at that point, we can conclude that this function is continuous for every integer, and since the floor and fractional part functions are only discontinuous at integer values, the function is continuous everywhere.
Note that there are exceptions when it comes to calculating limits, but since all of the functions in the question would be defined and continuous for x>1 were the floor and fractional part functions replaced with x, we can safely ignore problems like undefined or indeterminate points.
Now lets go through the functions one by one with this new technique:
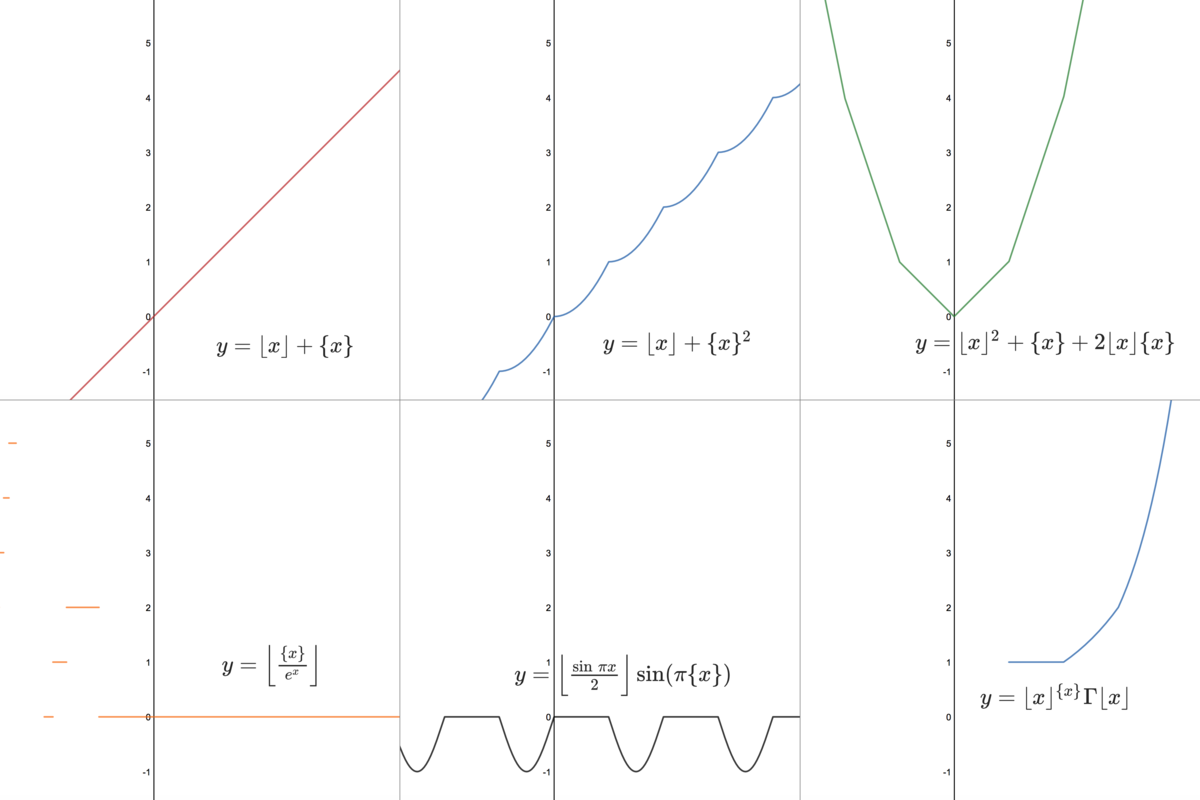
Case 1: y = ⌊ x ⌋ + { x }
This is proven above, but it's actually also trivial, because ⌊ x ⌋ + { x } = x , and y = x is obviously continuous everywhere.
Case 2: y = ⌊ x ⌋ + { x } 2
We can prove this using the method above: x → k + lim ⌊ x ⌋ + { x } 2 = k + 0 2 = k x → k − lim ⌊ x ⌋ + { x } 2 = k − 1 + 1 2 = k Since the two limits are equal, and the function is continuous for non-integer values of x, the function is continuous for x>1.
Case 3: y = ⌊ x ⌋ 2 + { x } + 2 ⌊ x ⌋ { x }
Be careful: This looks like a perfect square, but not quite, so again we cannot rearrange it to give Case 1. x → k + lim ⌊ x ⌋ 2 + { x } + 2 ⌊ x ⌋ { x } = k 2 + 0 + k ( 0 ) = k 2 x → k − lim ⌊ x ⌋ 2 + { x } + 2 ⌊ x ⌋ { x } = ( k − 1 ) 2 + 1 + 2 ( k − 1 ) ( 1 ) = k 2 − 2 k + 1 + 2 k − 2 = k 2 Since the two limits are equal, and the function is continuous for non-integer values of x, the function is continuous for x>1.
Case 4: y = ⌊ e x { x } ⌋
For this one, we will use a different technique. Note that for x>1, {x} is less than e x and both functions are positive. Therefore for all x>1, 0 < e x { x } < 1 . This means that when we take the floor of this value, we will always get 0. This is obviously continuous, because it is a straight line.
Case 5: y = ⌊ 2 sin π x ⌋ sin ( π { x } )
The floor surrounding a function is an issue, because it may be possible for ⌊ 2 sin π x ⌋ to be discontinuous at a non-integer value of x. 2 sin π x is a continuous function with a range between -1/2 and 1/2, and so ⌊ 2 sin π x ⌋ always equals either 0 or -1. The discontinuity occurs when we cross the x-axis, i.e. when 2 sin π x = 0 . We find that this only occurs at integer values of x, so we can continue with the algebraic solution. We actually only need to consider the fractional part function for this, as the sin ( π { x } ) becomes zero in both cases and eliminates everything else: x → k + lim ⌊ sin π x ⌋ sin ( π { x } ) = ⌊ sin π x ⌋ sin ( π ( 0 ) ) = ⌊ sin π x ⌋ × 0 = 0 x → k − lim ⌊ sin π x ⌋ sin ( π { x } ) = ⌊ sin π x ⌋ sin ( π ( 1 ) ) = ⌊ sin π x ⌋ × 0 = 0 Since the two limits are equal, and the function is continuous for non-integer values of x, the function is continuous for x>1.
Case 6: y = ⌊ x ⌋ { x } Γ ⌊ x ⌋
Note here that the gamma function is undefined for zero and negative integers. This does not matter, as we are only concerned with x>1, for which the gamma function is both defined and continuous. This solution requires a special property of the gamma function: x Γ ( x ) = Γ ( x + 1 ) x → k + lim ⌊ x ⌋ { x } Γ ⌊ x ⌋ = k 0 Γ ( k ) = Γ ( k ) x → k − lim ⌊ x ⌋ { x } Γ ⌊ x ⌋ = ( k − 1 ) 1 Γ ( k − 1 ) = ( k − 1 ) Γ ( k − 1 ) = Γ ( k ) Since the two limits are equal, and the function is continuous for non-integer values of x, the function is continuous for x>1.
So the answer is all 6 of the functions are continuous for x>1. This is what each of the functions looks like when graphed: