Weird Figure
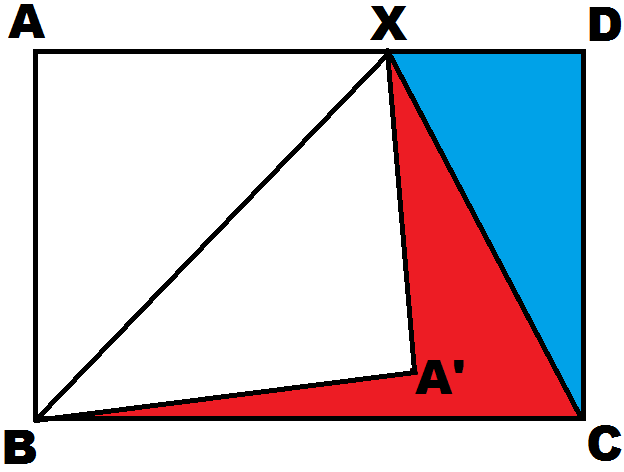
In the above figure A B C D is a rectangle. X is any point on segment A D . Point A ′ is the reflection of point A on B X . Then find the ratio of the area of red region to the area of blue region. Give your answer to correct two decimal places.
The answer is 1.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Moderator note:
Good observation about the regions.
The proof of B X C = A B X + D C X could be shown more intuitively by drawing the perpendicular from X to B C and noting that it divides the rectangle into two pairs of congruent triangles, which is how I first learnt that Δ = 2 1 b h . Interesting question!
I solved this by taking the limiting case X → A . The white area approaches zero; the line CX approaches the diagonal CA, dividing the rectangle into two congruent triangles ABC and ADC.
Hey it came out very nicely in the end 1 . 0 0 0 0 . I went with coordinates as reflection is simpler there. Anyway great problem
When I find the answer 1 , at first I'm not sure if I'm correct since you ask to give answer correct to 2 decimal places!
Log in to reply
I intentionally put it so that the answer cannot be guessed easily.
Using A B = C D and A D = A X + D X , we note that:
[ A B X ] + [ D C X ] = 2 1 ⋅ A B ⋅ A X + 2 1 ⋅ C D ⋅ D X = 2 A B ( A X + D X ) = 2 A B ⋅ A D = 2 [ A B C D ]
⇒ [ A B C D ] = 2 ( [ A B X ] + [ D C X ] ) ⇒ [ A B X ] + [ D C X ] + [ B X C ] = 2 ( [ A B X ] + [ D C X ] ) ⇒ [ B X C ] = [ A B X ] + [ D C X ] ⇒ [ B A ′ X ] + red region = [ A B X ] + [ D C X ]
Since A ′ is reflection of A in B X we easily have Δ B A X ≅ Δ B A ′ X ⇒ [ B A X ] = [ B A ′ X ] and using this fact from the above equation we have:
[ B A X ] + red region = [ A B X ] + [ D C X ] ⇒ red region = [ D C X ] = blue region
Since they are equal, their ratio is simply 1 .