Weird Incircle
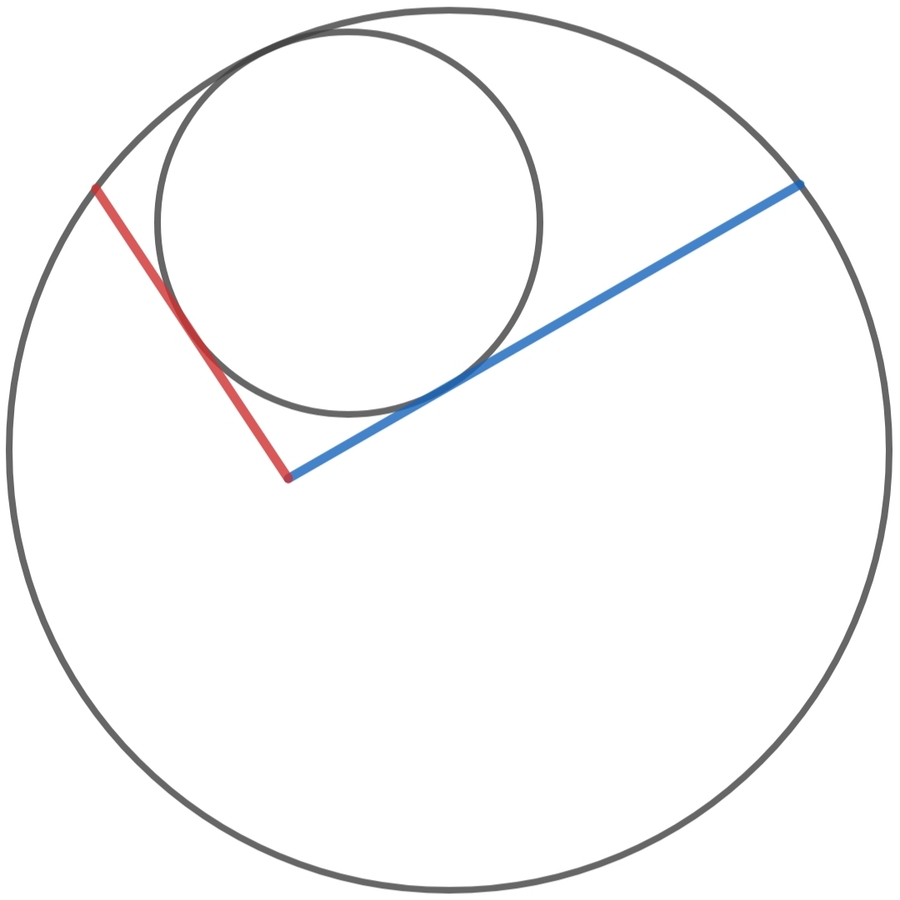
The given figure shows two line segments and a circle drawn inside a bigger circle.
The line segments have lengths and units. The radius of the bigger circle is units. The distance between the two upper ends of the line segments is units.
Find the radius of the small inscribed circle.
The answer is 3.9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
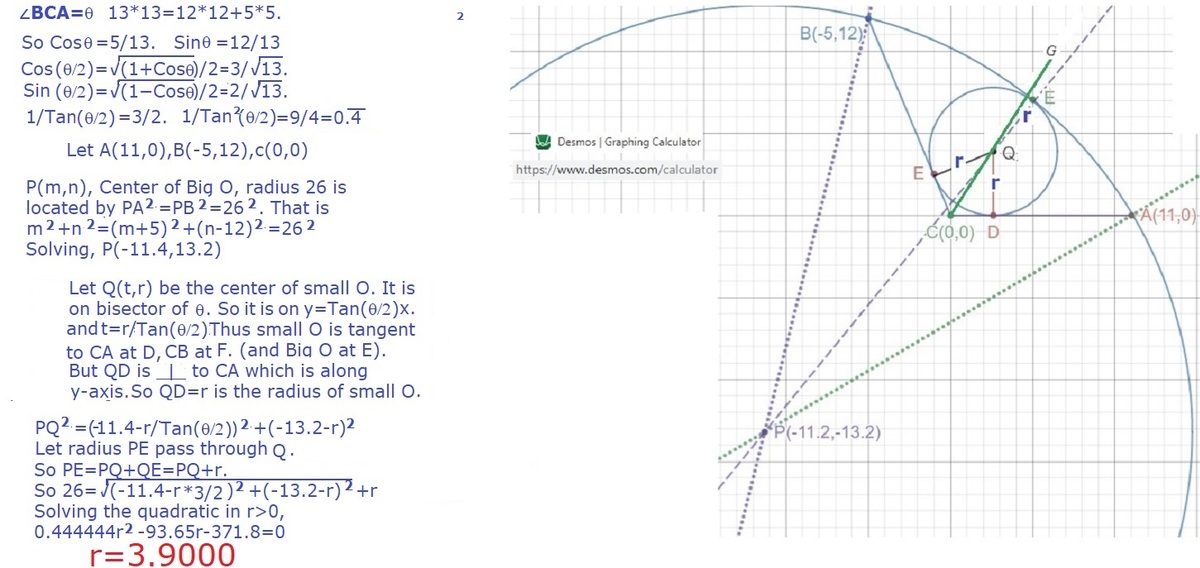
Although this is a special case of the general sangaku, this particular problem can be solved a little more simply. The centre of the big circle lies on the perpendicular bisector of A B . If we put the origin of our coordinate system at the midpoint of A B , so that A ( − 1 0 , 0 ) and B ( 1 0 , 0 ) , then the centre Q of the large circle has coordinates ( 0 , − 2 4 ) . We also note the right-angled triangle A B D , which is similar to a ( 3 , 4 , 5 ) triangle with third coordinate D ( 5 1 4 , − 5 4 8 ) . The triangle B C D is a ( 5 , 1 2 , 1 3 ) triangle, giving C ( − 5 6 , − 5 3 3 ) , so that A C = 1 1 and B C = 1 3 .
The incentre I of the triangle A B C is given by the formula O I = 4 4 1 [ 2 0 O C + 1 3 O A + 1 1 O B ] and hence I has coordinates ( − 1 , − 3 ) . Thus a general point X on the angle bisector of ∠ A C B has position vector O X = 5 1 ( λ − 6 ) i + 5 1 ( 1 8 λ − 3 3 ) j for λ ≥ 0 , and the distance of this point from the lines A C and B C is 3 λ . We therefore need to find the value of λ such that 3 λ = 2 6 − Q X , and hence 2 6 − 3 λ 1 0 0 λ 2 + 7 0 2 0 λ − 9 2 9 5 5 ( 1 0 λ − 1 3 ) ( 2 λ + 1 4 3 ) = 5 1 ( λ − 6 ) 2 + ( 1 8 λ + 8 7 ) 2 = 0 = 0 and hence the radius of the smaller circle is 3 λ = 1 0 3 9 .