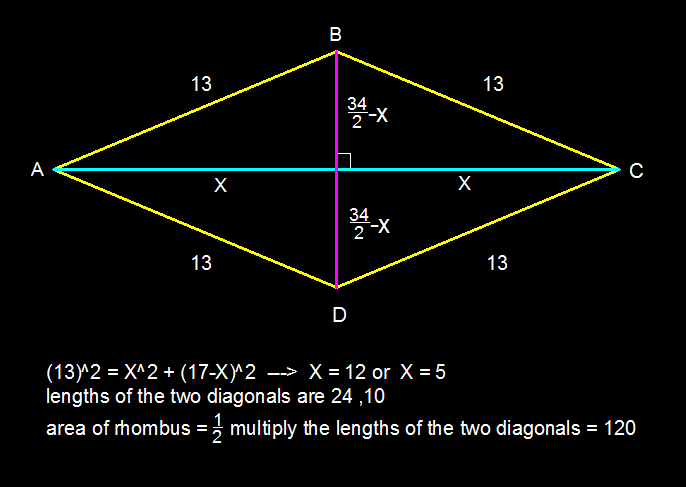
Weird square

In a regular rhombus all sides are the same length. The diagonals of any rhombus are perpendicular. 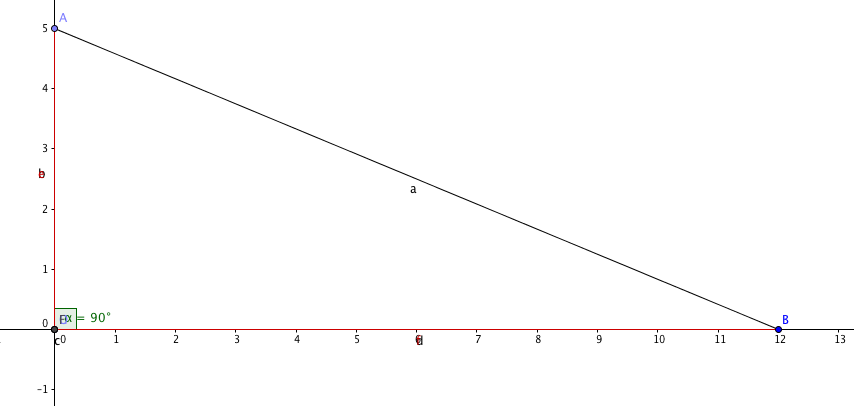By having perpendicular diagonals ( $90º$ ) and same length sides, we see that 4 right triangles with hypotenuse 13 are inscribed. Lets name each cathetus $a$ and $b$ , then $a ≠ b$ because if they were equal, our rhombus would be a square. $a ≠ b$ , $a^2 + b^2 = 13^2$ $=>$ $a^2 + b^2 = 169$ The only positive values that can be $a$ and $b$ are $a=5$ or $12$ and $b=5$ or $12$ We know $2a = AC$ and $2b=DB$ The area of a rhombus can be obtained by the product of its diagonals divided by two. Thus, $AC * DC *1/2 =120$ ∴ $Area = 120$