Weird wheels in Tonyland!
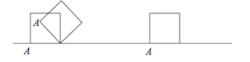 In Tonyland, cars have square wheels, of side length 60cm. The wheels rotate without sliding on the ground. If the distance traveled by the point A in a wheel spin is written as
a
π
+
b
2
π
, what is the value of
a
+
b
?
In Tonyland, cars have square wheels, of side length 60cm. The wheels rotate without sliding on the ground. If the distance traveled by the point A in a wheel spin is written as
a
π
+
b
2
π
, what is the value of
a
+
b
?
The answer is 90.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
1 s t r o t a t i o n = 4 2 × 6 0 π = 3 0 π
2 n d r o t a t i o n = 4 2 × 6 0 2 π = 3 0 2 π
3 r d r o t a t i o n = 4 2 × 6 0 π = 3 0 π
4 t h r o t a t i o n = 0
Total distance traveled
D = [ 3 0 π + 3 0 2 π + 3 0 π + 0 ] = 6 0 π + 3 0 2 π
a + b = 9 0
There are four rotations, one around each corner of the square. In the first one, A describes a quarter-arc of the circle of radius 6 0 centered at the right bottom corner. In the second one, A describes a quarter-arc of the circle of radius 6 0 2 centered at the right bottom corner. In the third one, A describes a quarter-arc of the circle of radius 6 0 centered at the right bottom corner. In the fourth one A is the right bottom corner and hence does not move.
The sum is therefore 3 0 π + 3 0 π 2 + 3 0 π = 6 0 π + 3 0 π 2 . So a = 6 0 , b = 3 0 , a + b = 9 0 .