Welcome 2016! Part 16

Algebra Level 4

Let $x$ and $y$ be non - negative real numbers such that

$\large x^3+y^3+(x+y)^3+30xy=2000$

Find the value of $x+y$ .

The answer is 10.

3 solutions

Nuttapat Bk
Dec 23, 2015

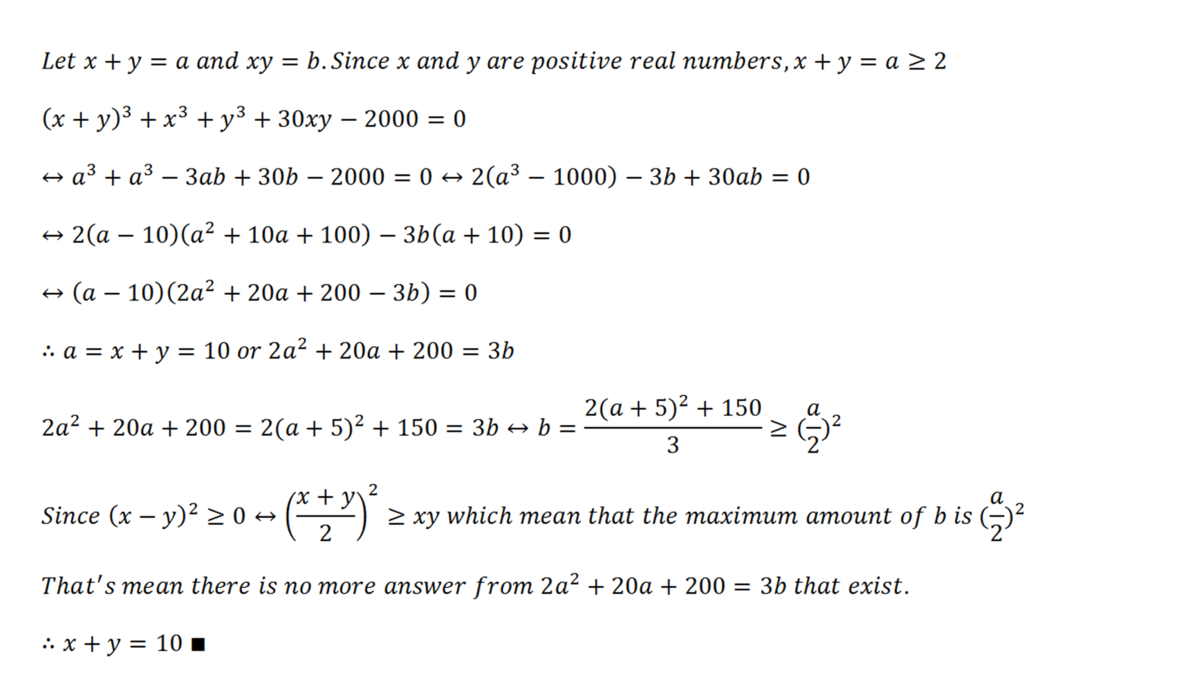
I disagree with the first line. It is not true that $a \geq 2$ . However, that is not used elsewhere in your solution.

Calvin Lin Staff - 5 years, 5 months ago

Yes. I just see that both x and y are just positive real numbers, not positive integers. So it should be a>=0. But anyway it wasn't used in the solution.

Nuttapat Bk - 5 years, 5 months ago

Siddhant Chaudhari
Dec 23, 2015

Let x+y =s. Then on use of some simple identies and expansion, we get the equation 2s^{3} -3sxy +30xy -2000 =0 Thus, the possible roots should divide 30xy -2000 which is the constant term of the equation in s. Thus possible roots are 1 or 2 or 5 or 10. Now the equation is equal to s^{3}-3xy(s-10)=2000. Try the obtained roots and u will see that 10 satisfies the equation. A bit tedious, but it works.

Akhil Bansal
Dec 24, 2015

Jee Style
Given equation is an identity (for $x,y \geq 0$ )

So, substituting $x = 0$
$\large 0^3 + y^3 + (0 + y)^3 + 30*0*y= 2000$ $\large y = 10$ $\large \therefore x + y = 0 + 10 = \boxed{10}$

Moderator note:

This solution doesn't make sense. The given equation is not an identity .

I guess what you are trying to say is that the answer is independent of $x+y$ . If so, make that explicit instead and state that you do not have the general solution.

To the challenge master: Can you post the perfect general solution?

Swapnil Das - 5 years, 5 months ago

Welcome 2016! Part 16

The answer is 10.

3 solutions

Moderator note:

0 pending reports