Well, a quadrilateral inside a quadrilateral
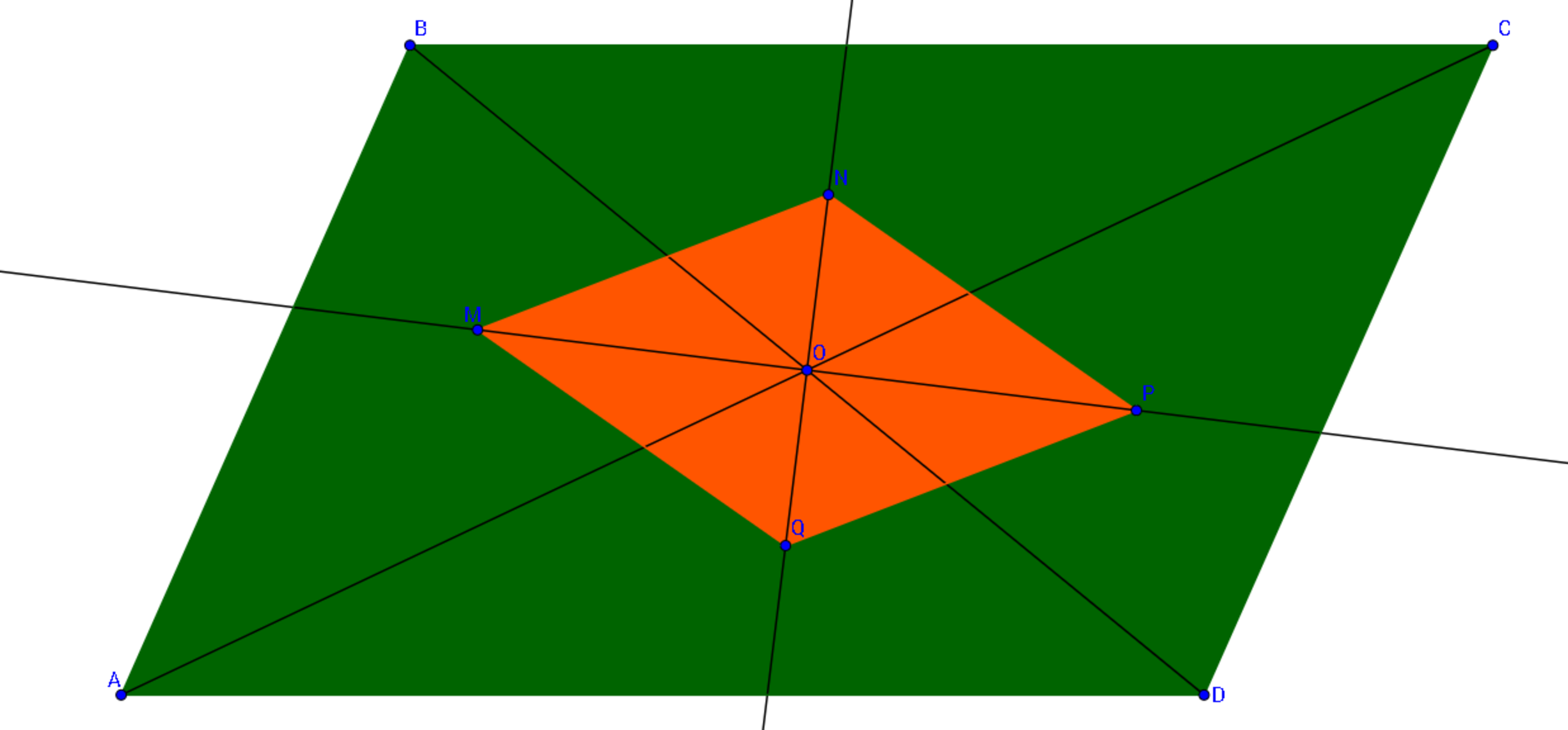 is a parallelogram.
are the incenters of
. What kind of quadrilateral is
?
is a parallelogram.
are the incenters of
. What kind of quadrilateral is
?
Choose the most specific and correct answer.
This is part of the series: " It's easy, believe me! "
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
O M is angle bisector ⟹ ∠ B O M = ∠ A O M ⋯ E q . 1 O Q is angle bisector ⟹ ∠ D O Q = ∠ A O Q ⋯ E q . 2 adding both equation we get, ⟹ ∠ B O M + ∠ D O Q = ∠ A O M + ∠ A O Q = ∠ M O Q ⟹ ∠ B O M + ∠ D O Q + ∠ M O Q = 2 ∠ M O Q ⟹ 2 ∠ M O Q = 1 8 0 ∘ ⟹ ∠ M O Q = 9 0 ∘ . ⟹ M P ⊥ N Q Diagonals of quadrilateral M N P Q intersect at 9 0 ∘ . ⋯ Statement 1
Δ A O D and Δ C O B are congruent [ ∵ A D = C B , A O = O C and D O = O B ] ⟹ O Q = O N [ ∵ Q and N are corresponding in-centres of the triangles ] Similarly O M = O P Diagonals of quadrilateral M N P Q bisect each other. ⋯ Statement 2
Combining both the statements, Diagonals of quadrilateral M N P Q bisect each other at 9 0 ∘ . and this is the definition of rhombus . ⟹ M N P Q is a rhombus .