Well, I Guess That Works
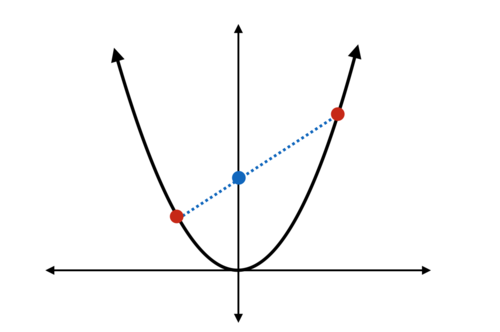 I'm trying to do a calculation with positive numbers
a
and
b
.
All I have is a graph of
y
=
x
2
and some string. I connect the points where
x
=
a
and
x
=
−
b
,
and see where my string touches the
y
-axis for my result!
I'm trying to do a calculation with positive numbers
a
and
b
.
All I have is a graph of
y
=
x
2
and some string. I connect the points where
x
=
a
and
x
=
−
b
,
and see where my string touches the
y
-axis for my result!
What calculation am I doing?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Short trick: Let a = b . Then a 2 = b 2 and the line joining the two points is always parallel to the x axis. The string touches the y axis at y = a × a for all values of a . Substitute a = b in all options. The only option satisfying the condition is a × b
Looking at the figure,
When a=0, answer has to be 0. When b=0, answer has to be 0.
When a is fixed & b is moving (or vice-versa), y intercept is proportional to a (or b). Which makes the answer ab .
If the intercept is ( 0 , q ) , we want a − 0 a 2 − q = a − ( − b ) a 2 − b 2 = a − b so a 2 − q = a 2 − a b and q = a b .
Solution 1: Draw horizontal lines at both the points. The lines intersect the y axis at y = a 2 and y = b 2 . Let's name the points ( 0 , a 2 ) and ( 0 , b 2 ) A and B respectively. Let the string intersect the y axis at ( 0 , c ) and this point is named C . Then C divides the line segment A B in the ratio a : − b .
Using the section formula , we can find the coordinates of C .
c = a + ( − b ) a × b 2 + ( − b ) × a 2 = a − b ( a × b ) ( a − b ) = a × b □
Solution 2: Let's find the equation of the line formed by the string. Since we are know the coordinates of two points on the line, we can use the point-point form . The two points on the line are ( a , a 2 ) and ( − b , ( − b ) 2 ) .
The slope of the line is m = a − ( − b ) a 2 − b 2 = a + b a 2 − b 2 = a − b . Hence the equation of the line is
( y − y 1 ) ( y − a 2 ) = m ( x − x 1 ) = ( a − b ) × ( x − a )
To find the y intercept, we set x = 0 .
y − a 2 y − a 2 y = ( a − b ) × ( − a ) = − a 2 + a × b = a × b □