Well Known Phenomenon
Consider a spring-mass system. One end of the spring is fixed at the origin of the X-Y plane while the other end is attached to a mass which can move along the X-axis only. The instantaneous coordinate of the mass is x ( t ) . A time-varying force F ( t ) starts acting on the mass at time t = 0 :
F ( t ) = sin 4 t
The initial position of the mass is x ( 0 ) = 2 and the mass is at rest at time t = 0 . Compute the total energy E of the mass (kinetic + potential) at time t = 2 9 π . The answer is of the form:
E = 3 2 ( a π − b ) c
Here, a , b and c are positive integers. Compute a + b + c .
Note:
-
Stiffness of the spring K = 1 6
-
The natural length of the spring L o = 1
-
Mass M = 1
-
Gravity is absent.
-
The spring force is governed by Hooke's law.
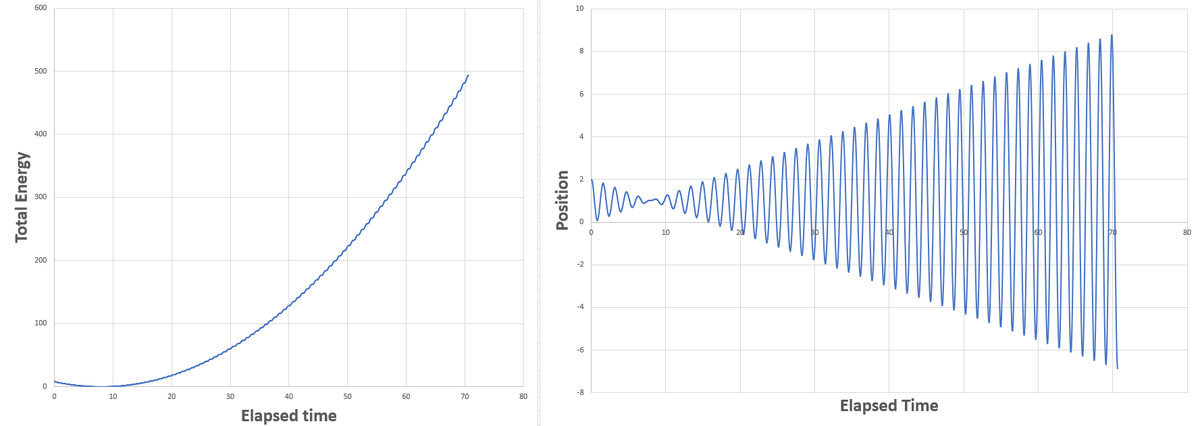
Bonus: Explain the well known physical phenomenon being demonstrated through this problem. Also, plot the total energy of the mass as a function of time and explain it. Plot up to a larger instant of time. Something unusual happens initially. Why?
The answer is 27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
And I am impressed by @Steven Chase he has explained the phenomenon very accurately.
@Karan Chatrath
Sorry sir. You were right that I am lucky to get the answer.
Above in the solution, I have updated it.
Please forgive me.
Thanks in advance.
Thanks for the solution. Yes, this looks correct to me now.
Log in to reply
@Karan Chatrath
and I am posting solution through Laplace also within 10min.
And forgive me also
@Karan Chatrath
through Laplace I am not getting correct equation of
x
(
t
)
as above
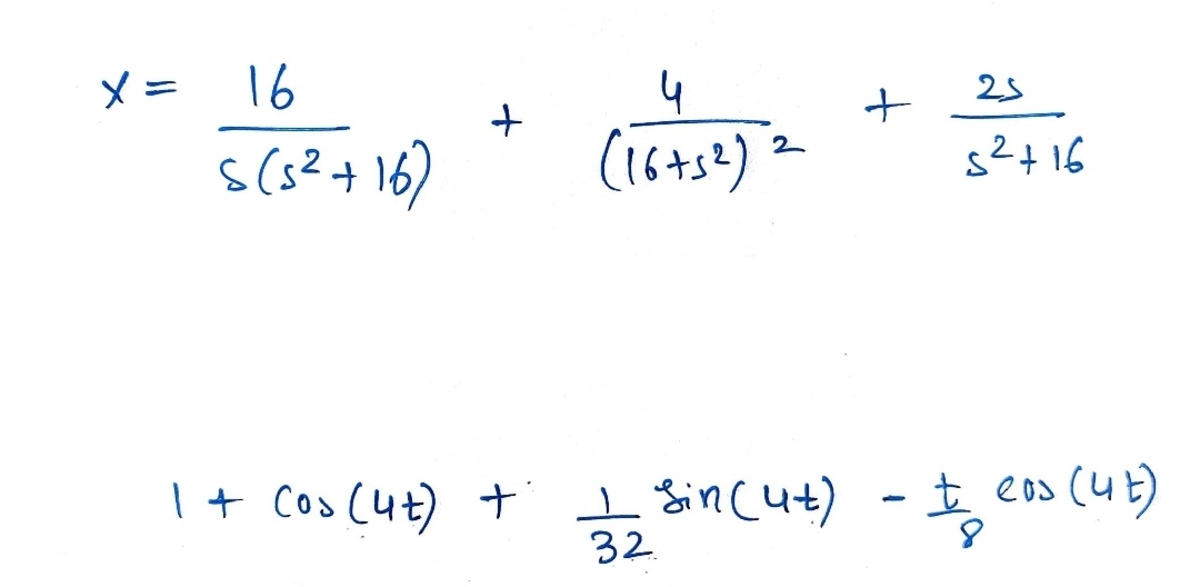
@Karan Chatrath
How can this problem get Level 2
At least it should be 4??
I will let someone else post a detailed solution. The phenomenon is known as "resonance".
ω = m k = 4
The forcing function has exactly the same frequency as the natural frequency of the system. So there are oscillations that continue to grow with time. As time increases, the total energy grows without bound. Plots of position and energy over time are included below. There is an initial period in which the mass-spring system is "synchronizing" with the external force. The total system energy momentarily decreases during this period. I think of it as the external force bending the system to its will. I liken this to hitting a tennis ball that has been served by the opposing player. To get the ball to go where you want it to go, you must first undo whatever velocity or energy it already has before imparting some velocity in the direction of your choosing.
As a side note, if you play a sound at the resonance frequency of a glass cup, the cup walls will oscillate with increasing amplitude until the cup eventually shatters.
Thanks for the insightful explanation.
@Steven Chase
your explanation is vey nice and beautiful. (Upvoted)
BTW I have uploaded a very detailed solution.
@Steven Chase is the new problem uploaded now??
The given information makes it clear that initially (I. e., at t = 0 ) the mass is at it's extreme position. It is simple to show that the time period of motion of the mass is T = 2 π K M = 2 π
So, at time t = 2 9 π = 9 T , the mass will be at it's extreme position and it's K.E. will be zero. Hence it's total mechanical energy will be it's P. E., which is equal to 2 1 K x m a x 2
Solution to the differential equation of motion of the mass for the given initial conditions is
x = ( 1 − 8 t ) cos ( 4 t ) + 3 2 1 sin ( 4 t ) ⟹ x m a x = 1 − 1 6 9 π at time t = 2 9 π
Hence the total energy is 3 2 ( 9 π − 1 6 ) 2 , a = 9 , b = 1 6 , c = 2 , a + b + c = 2 7 .
This is an example of forced undamped periodic motion of a mass-spring system. The frequency of the applied force ( 4 ) matches the natural frequency of oscillation of the system ( 4 ), and hence this is an example of a resonant oscillation. Due to inertia, the system takes some time to cope up with the applied force to vibrate in resonance.
Very Nice Problem
The basic equation which I get − 1 6 ( x − 1 ) + s i n ( 4 t ) = x ¨
Solving the above differential equation I get x ( t ) = α s i n ( 4 t ) + β c o s ( 4 t ) − 0 . 1 2 5 t c o s ( 4 t ) + 1
Using initial conditions, we can find out α and β x ( 0 ) = 2 x ˙ ( 0 ) = 0
Which comes out to be x ( t ) = 3 2 s i n ( 4 t ) + 3 c o s ( 4 t ) − 0 . 1 2 5 t c o s ( 4 t ) + 1
Now substituting t = 2 9 π , in the above equation to find out the location of block, which comes out to be x ( 2 9 π ) = 1 6 3 2 − 9 π
Now differentiating the x ( t ) to find out velocity, which comes out to be x ˙ ( t ) = ( 0 . 5 t − 1 2 ) s i n ( 4 t )
Now putting t = 2 9 π to find out the velocity of the block which comes to be x ˙ ( 2 9 π ) = 0
Now the.equation of Energy is E = 2 1 M v 2 + 2 1 K y 2
where y is the extension in the spring.
And the local of block is 1 6 3 2 − 9 π and the natural length of spring is 1 so y = 1 6 3 2 − 8 π − 1 y = 1 6 1 6 − 9 π E = 0 + 2 1 1 6 y 2
Substituting value of y and simplifying gives E = 3 2 ( 1 6 − 9 π ) 2
As we know ( a − b ) 2 = ( b − a ) 2
Applying the above identity gives E = 3 2 ( 9 π − 1 6 ) 2
a + b + c = 2 7