Well, there is a lot of length bashing required!
There is a trapezium A B C D with parallel sides A B and D C and height 1. It is known that ∠ D A B = 6 ∘ and ∠ A B C = 4 2 ∘ . Point P is on side A B such that ∠ A P D = 7 8 ∘ and ∠ C P B = 6 6 ∘ .
What is the value of A D − B C + D P − C P ?
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
When you copy-paste my solution.
Log in to reply
well you might have also copy-pasted from some other source.
Awesome solution.
Log in to reply
Thanks!! well the credit should also go to sharky as he helped me.
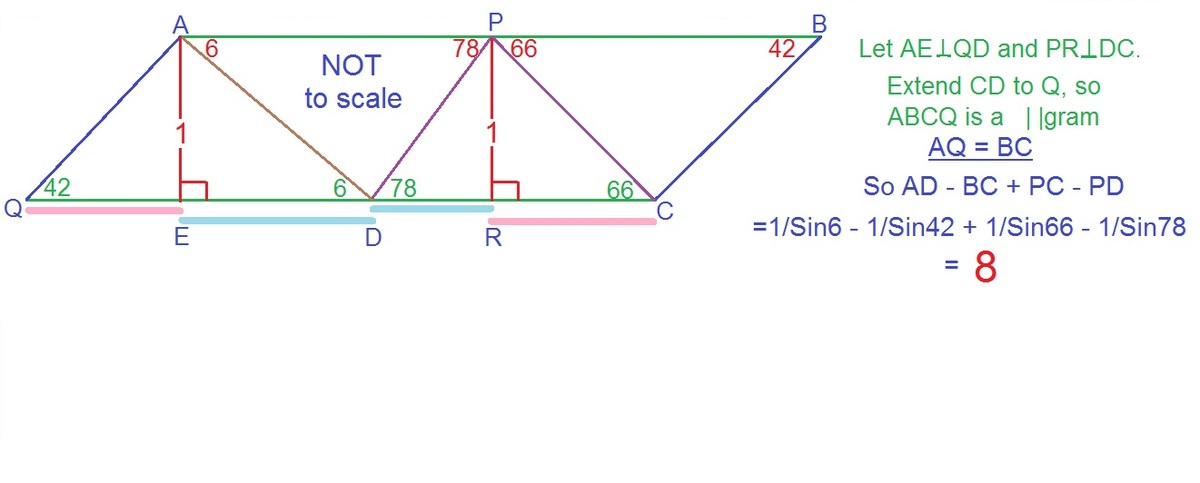
For some reason the sketch is coming small. Please magnify 200% or more.
A
D
−
B
C
+
P
C
−
P
D
=
S
i
n
6
1
−
S
i
n
4
2
1
+
S
i
n
6
6
1
−
S
i
n
7
8
1
=
8
link text
S i n 6 1 − S i n 4 2 1 + S i n 6 6 1 − S i n 7 8 1 = 8 ..How you solved this?
Log in to reply
I used calculator but one may go to link I have provided now.
did it the same
Drop perpendicular from P to DC at point Q. Creating Right Triangles PDQ and PCQ.
Sin(78) = 1/DP yielding DP = 1.022
Sin 66) = 1 / PC yielding PC = 1.095
Looking at Triangle PAD and using Law of Sines : 1.022 / Sin (6) = AD / sin (78) which yields AD = 9.564
Look at Triangle PBC and use Law of Sines : 1.095 / sin (42) = BC / sin(66) from which we obtain BC = 1.495
9.564 -1.495 + 1.022 - 1.095 = 7.996 or 8
Use simple geometry, A D = csc 6 ∘ , B C = csc 4 2 ∘ , D P = csc 7 8 ∘ , C P = csc 6 6 ∘ ,
hence, A D − B C + D P − C P = csc 6 ∘ − csc 4 2 ∘ + csc 7 8 ∘ − csc 6 6 ∘ = 8
How to drive formula
Dropping a perpendicular (of length 1) from D to AP, and similarly from C to BP, we see that:
AD = cosec 6° DP = cosec 78° BC = cosec 42° CP = cosec 66°
Notice that, for x = 6°, 78°, −42°, −66°, and 30°, sin 5x = ½. We now express sin 5x in terms of sin x.
De Moivre's theorem states that for any real number x and any integer n,
cos nx + i sin nx = (cos x + i sin x)n
Setting n = 5, expanding the right-hand side using the binomial theorem, and equating imaginary parts, we obtain
sin 5x = sin5x − 10 sin3x cos2x + 5 sin x cos4x = sin5x − 10 sin3x (1 − sin2x) + 5 sin x (1 − sin2x)2, since sin2x + cos2x = 1 = 16 sin5x − 20 sin3x + 5 sin x
This result can also be obtained by means of trigonometric identities. Setting s = sin x, it follows that the five distinct real numbers, sin 6°, sin 78°, −sin 42°, −sin 66°, and sin 30° = ½, (1) are roots of the equation 16s^5 − 20s^3 + 5s = ½, or, equivalently, of 32s^5 − 40s^3 + 10^s − 1 = 0. (2) By the Fundamental Theorem of Algebra, (2) has exactly five roots, up to multiplicity, and hence these must be precisely the distinct roots identified in (1).
Since s = ½ is a root of (2), the equation factorizes: (2s − 1)(16s^4 + 8s^3 − 16s^2 − 8s + 1) = 0, yielding the quartic equation whose roots are sin 6°, sin 78°, −sin 42°, and −sin 66°.
As s = 0 is not a root of this quartic equation, we may divide by s4, and, setting t = 1/s, obtain t4 − 8t3 − 16t2 + 8t + 16 = 0, an equation whose roots are cosec 6°, cosec 78°, −cosec 42°, and −cosec 66°.
By Vieta's formulas, the sum of the roots of this equation is 8.
Thus, AD -BC+DP - CP = 8.
Credit should also go to @Sharky Kesa