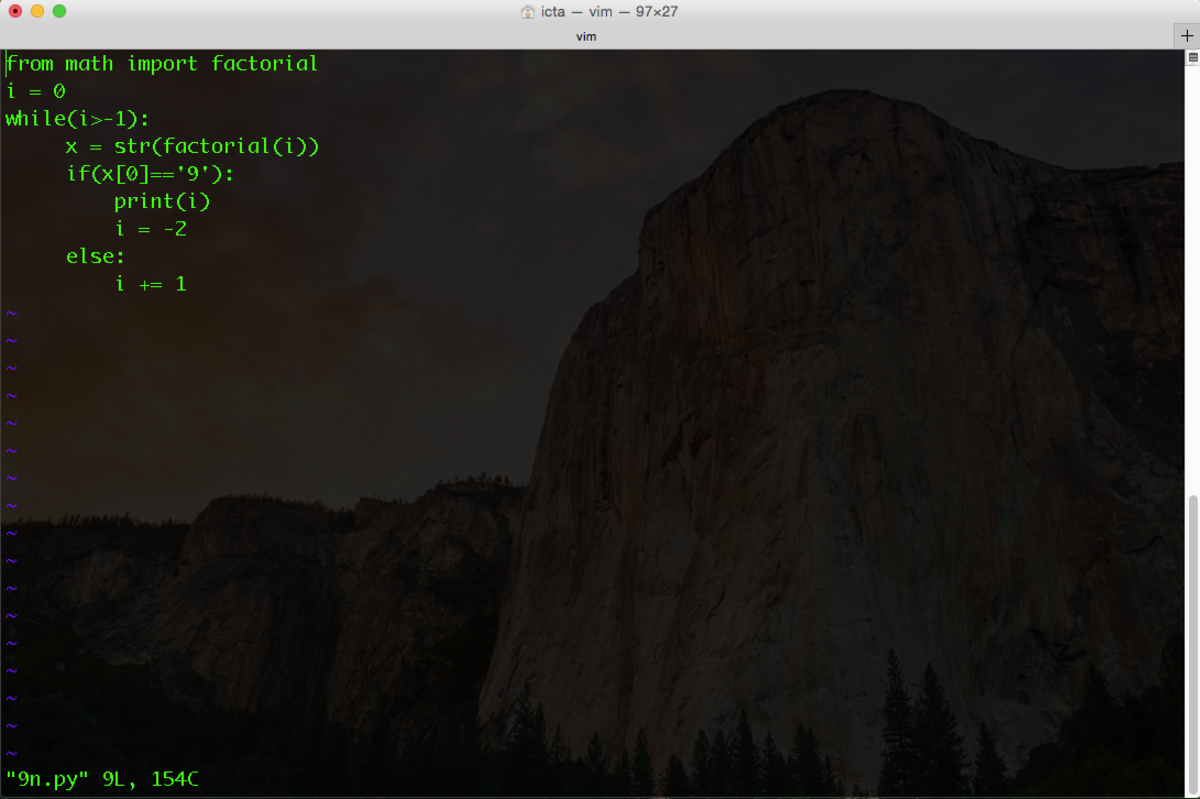
Factorial With All Of The Digits!

Computer Science Level 3

What is the smallest non-negative integer n n for which n ! n! starts with the digit 9?


The answer is 96.

View wiki
Vishnu Bhagyanath by Vishnu Bhagyanath , 23, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

5 solutions 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
 
def fact(n):
    ans = 1
    while n>0:
        ans *= n
        n -= 1
    return ans    

n = 2
while True:
    temp = str( fact(n) )
    if temp[0] == '9':
        print n
        break
    n += 1

3 Helpful 0 Interesting 0 Brilliant 0 Confused

Here 's a C++ solution using a mathematical approach which is that the first digit of a positive integer n n is given by,

First digit ( n ) = ⌊ 1 0 { log ⁡ 10 ( n ) } ⌋ \large\textrm{First digit }(n)=\left\lfloor 10^{\{\log_{10}(n)\}}\right\rfloor

where { ⋅ } \{\cdot\} is the fractional part function and ⌊ ⋅ ⌋ \lfloor\cdot\rfloor is the floor function . Proving the above claimed formula is quite easy (using basic exponent laws and logarithm laws) and is left as an exercise to the reader.

Prasun Biswas - 5 years, 10 months ago
Bill Bell
Sep 16, 2015

Calculating factorials is expensive, and so is converting integers to strings. I therefore avoided both of these calculations. (Not that it matters in this case!) 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
 
def biggest_digit(n):
    while n>=10:
        n = n / 10
    return n

n=1
f=1
while True:
    n+=1
    f*=n
    if biggest_digit(f)==9:
        print n
        break

2 Helpful 0 Interesting 0 Brilliant 0 Confused
Ícaro Augusto
Aug 19, 2015

Ruby 

def factorial(n)
  i = n
  until (i == 1) do
    i -= 1
    n = n * i
  end
  n
end



x = 0
h = 0
while x == 0 do
  h += 1
  a = factorial(h).to_s
  if a[0] == "9"
    x = 1
  end  
end

puts h
gets.chomp
1 Helpful 0 Interesting 0 Brilliant 0 Confused
Arulx Z
Aug 6, 2015 
1
2
3
4
5
 
>>> import math
>>> n = 1
>>> while str(math.factorial(n))[0] != '9':
        n += 1
>>> print n

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Simple standard approach.

I have a mathlab/octave solution for those who are interested :

clear all;

format long

number = 0;

for i = 1 : 170 

number = factorial(i);

do 

number = number/10;

until (number <10)

if (floor(number) == 9)

disp ("The wanted number is :"), disp (i)

break;

endif

Tom Van Lier - 5 years, 10 months ago
Aareyan Manzoor
Aug 30, 2015

python 3 . returns 96

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...