RLC with DC current
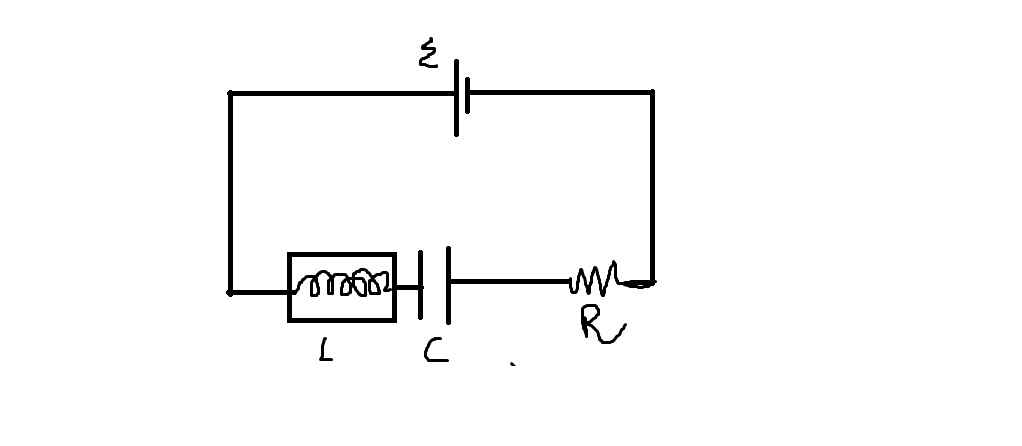
Here we have this simple situation and before t=0, nothing was connected and neither charged none had any energy stored in it initially. At t=0, the situation begins and current starts flowing into the wires.
If the current changes with time as
i ( t ) = c 1 e λ 1 t + c 2 e λ 2 t + k , where c 1 , c 2 and k are contants.
Find the value of 2 λ 1 × λ 2 1 .
Given
- R = 1 Ohm , C = 4 F and L = 2 H .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
We want to find both natural frequencies λ 1 , 2 of the circuit. Calculate a transfer function, e.g. per voltage divider: H ( s ) = V ( s ) U c ( s ) = s L + R + s C 1 ± s C 1 = s 2 C L + s R C + 1 ± 1 = C L ± 1 ⋅ s 2 + s L R + C L 1 1 = ! C L ± 1 ⋅ ( s − λ 1 ) ( s − λ 2 ) 1 Numerator and denominator of H ( s ) are relatively prime, so the denominator zeroes are all natural frequencies. Comparing coefficients, we get 2 λ 1 λ 2 1 = 2 C L = 4 s 2
DSolve [ { 2 i ′ ( t ) + 4 1 ∫ 0 t i ( x ) d x + i ( t ) = 1 , i ( 0 ) = 0 } , i , t ] ⇒ i ( t ) = 2 e − 4 t sin ( 4 t ) ⇒ i e ( − 4 1 − 4 i ) t − i e ( − 4 1 + 4 i ) t
2 8 1 1 ⇒ 4
Let us call V ( t ) the voltage supply, a step in this case. The differential equation will be:
V ( t ) = R i ( t ) + L d t d i ( t ) + C 1 ∫ 0 t i ( τ ) d τ
Assuming that the amplitude of the voltage step is V 0 and applying Laplace Transform :
s V 0 = ( R + L s + C s 1 ) I ( s )
I ( s ) = s 2 + L R s + L C 1 L V 0
For the given values:
I ( s ) = s 2 + 0 . 5 s + 0 . 1 2 5 0 . 5 V 0
The roots of s 2 + 0 . 5 s + 0 . 1 2 5 are actually complex, which leads to a sine:
I ( s ) = ( s + 0 . 2 5 ) 2 + 0 . 0 6 2 5 0 . 5 V 0
I ( s ) = 2 V 0 ⋅ ( s + 0 . 2 5 ) 2 + 0 . 0 6 2 5 0 . 2 5
Since L ( e − a t sin ( ω t ) ) = ( s + a ) 2 + ω 2 ω
i ( t ) = 2 V 0 e − 0 . 2 5 t sin ( 0 . 2 5 t )
Which acutally makes sense. After the unit step, the voltage is DC, and current must tend to 0 , since capacitors in DC current are an open circuit. So, there shall be no constant term in the current value. Or, k = 0 .
Buf, if we consider the complex values of s:
I ( s ) = s 2 + 0 . 5 s + 0 . 1 2 5 0 . 5 V 0
j is the imaginary unit:
I ( s ) = s + 0 . 2 5 + 0 . 2 5 j j V 0 + s + 0 . 2 5 − 0 . 2 5 j − j V 0
i ( t ) = j V 0 e − ( 0 . 2 5 + 0 . 2 5 j ) t − j V 0 e − ( 0 . 2 5 − 0 . 2 5 j ) t
Which is the same as the expression above, with the sine and the exponential, just written in another form. So, in this case:
k = 0 , λ 1 = − 0 . 2 5 − 0 . 2 5 j , λ 2 = − 0 . 2 5 + 0 . 2 5 j , 2 λ 1 × λ 2 1 = 4