How high can it go?
Let x and y be real numbers. Find the maximum value of x − y if 2 ( x 2 + y 2 ) = x + y
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Oh thats a clever factoring and geometrical interpretation!
+1!!
Yup!! Did it in the same way. Geometry always comes in handy.
x + y x + y − ( x + y ) 2 Let ( x + y ) = t , ( x − y ) 2 f ′ ( t ) f ′ ( t ) f ′ ′ ( t ) ⟹ f ( 2 1 ) = 4 1 ( x − y ) 2 − 2 1 ≤ x − y Maximum = 2 ( x 2 + y 2 ) Given = 2 ( x 2 + y 2 ) − ( x 2 + 2 x y + y 2 ) = x 2 − 2 x y + y 2 = ( x − y ) 2 = f ( t ) = t − t 2 = 1 − 2 t = 0 ⟹ t = 2 1 = − 2 < 0 is a maxima ≤ 4 1 ≤ 2 1 value of x − y = 2 1
2 ( x 2 + y 2 ) = x + y = > 2 ( x + y ) 2 − 4 x y = x + y = > 4 x y = ( x + y ) − 2 ( x + y ) 2
( x − y ) 2 = ( x + y ) 2 − 4 x y = ( x + y ) − ( x + y 2 )
Using the Completing-Square Rule-
( x − y ) 2 = 4 1 − ( x + y − 1 / 2 ) 2
Maximum value occurs at x + y = 1 / 2 and maximum value of x − y = 2 1
You can directly use, 2 ( x 2 + y 2 ) = ( x + y ) 2 + ( x − y ) 2 .
2 ( x 2 + y 2 ) = x + y
⇒ ( x − 4 1 ) 2 + ( y − 4 1 ) 2 = 8 1 = ( x − 4 1 ) 2 + ( 4 1 − y ) 2
By Titu's Lemma ,
8 1 = ( x − 4 1 ) 2 + ( 4 1 − y ) 2 = 1 ( x − 4 1 ) 2 + 1 ( 4 1 − y ) 2 ≥ 2 ( x − y ) 2
⇒ ( x − y ) ≤ 2 1
With equality if ( x − 4 1 ) = ( 4 1 − y ) ⇒ x + y = 2 1
Very nice application of Titu's, I wouldn't have thought about this method.
Thanks for sharing, Ankit!!
2 ( x 2 + y 2 ) 2 ( ( x + y ) 2 − 2 x y ) 2 ( x + y ) 2 − 4 x y ( x + y ) 2 − 4 x y ( x − y ) 2 ( x − y ) = x + y = ( x + y ) = ( x + y ) = ( x + y ) − ( x + y ) 2 = ( x + y ) − ( x + y ) 2 = ( x + y ) − ( x + y ) 2
L H S maximum when R H S maximum.
R H S maximum when ( x + y ) = − 2 ( − 1 ) 1 = 2 1
Putting ( x + y ) = 2 1 , we have ( x − y ) = 2 1 − 2 1 2 = 4 1 = 2 1 = 0 . 5
From am-gm we get x 2 + y 2 = 2 1 and x + y = 1 , so we get maximum value of x − y = 2 1
Why can't it be x^2+y^2 = 2, x+y = 2?
I Got that from am gm
Log in to reply
AMGM of what numbers? x and y? Note that AMGM only works if x and y are non-negative real numbers, but in this case, this problem didn't state if x,y are non-negative or not.
No, This is AMGM of x 2 + y 2 and x + y becausa from this case x + y definite positive
Log in to reply
how do you know that x+y is positive? the question didn't state that.
2 ( x 2 + y 2 must positive so x + y also positive right? @Pi Han Goh
When x = y = 0 we can't Got maximum value of x − y . So x + y must positive. @Pi Han Goh
Log in to reply
if x+y = 0 must be positive, does that mean that both x and y must be positive? How do you know one of them can't be negative?
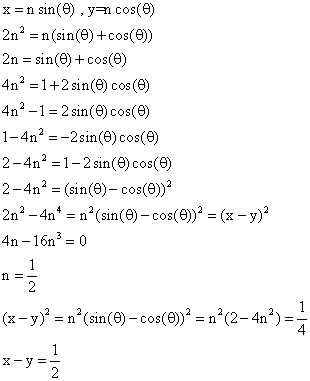
By completing squares, the given equation can be written as
x 2 − 2 x + y 2 − 2 y = 0 ⟹ ( x − 4 1 ) 2 + ( y − 4 1 ) 2 = 8 1 ,
which describes a circle with center ( 4 1 , 4 1 ) and radius 8 1 = 2 2 1 .
We can then let x − 4 1 = 2 2 1 cos ( θ ) and y − 4 1 = 2 2 1 sin ( θ ) .
From this we have that
x − y = 2 2 1 ( cos ( θ ) − sin ( θ ) ) = 2 1 ( 2 1 cos ( θ ) − 2 1 sin ( θ ) ) = 2 1 sin ( 4 π − θ ) .
As the maximum of the sine function is 1 , we see that the maximum of x − y is 2 1 = 0 . 5 .