What a Springy Parameterization!

Algebra Level 2

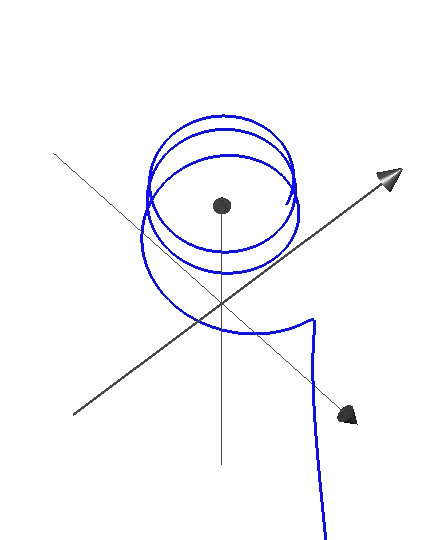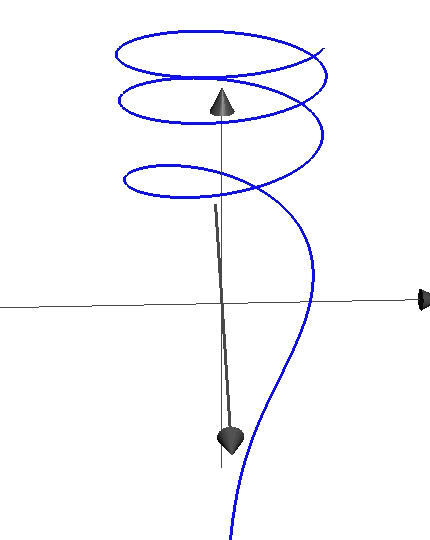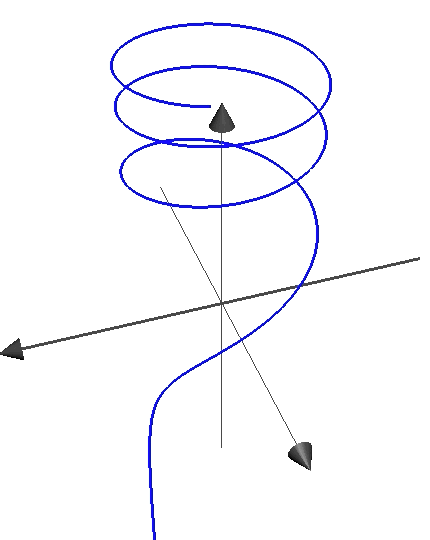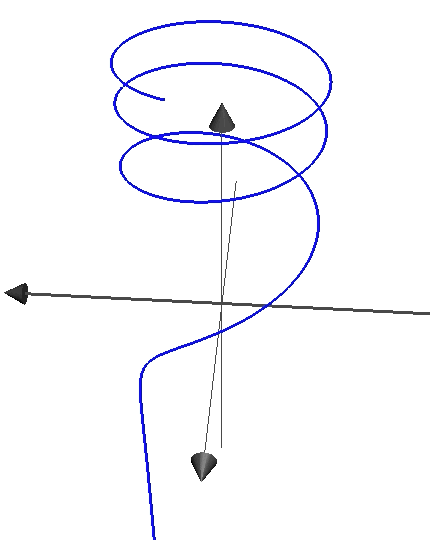
The parametric equations for the curve shown are { x = cos ⁡ ( t ) y = sin ⁡ ( t ) z = ? \begin{cases} x = \cos(t) \\ y = \sin(t) \\ z = \text{?} \end{cases} where t t ranges over ( 0 , 20 ) (0, 20) . Which function could z z be equal to?

t 2 t^2 ln ⁡ ( t ) \ln(t) sin ⁡ ( t ) \sin(t) t \sqrt{t}

View wiki
Clara Blackstone by Clara Blackstone , 32, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Clara Blackstone
Oct 13, 2015

The fact that the helix shown dips below the x y xy -plane indicates that z z should be able to take on negative values, so this rules out e t e^t and t \sqrt{t} . Lastly, we see that the z z value grows much more slowly as t t increases, which is indicative of z = ln ⁡ ( t ) z = \ln(t) .

9 Helpful 1 Interesting 0 Brilliant 0 Confused
Farhad Hasankhani
Feb 11, 2016

z can take infinitely large negative values eccording to the graph. Simply none of the functions t^2, sqrt(t) , and sint(t) has this property. So, the answer is : ln(t)

2 Helpful 0 Interesting 0 Brilliant 0 Confused
Kushagra Sharma
Oct 29, 2015

According to adaptive learning in this question at the bottom of the structure ring is open curvy like the 2d graph of logarithm so answer is ln(t)

1 Helpful 0 Interesting 0 Brilliant 1 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...