What Acute Angle You Have There!
A B C is an acute triangle with ∠ B C A = 3 5 ∘ . Denote the circumcenter of A B C as O and the orthocenter of A B C as H . If A O = A H , what is the value of ∠ A B C (in degrees)?
Details and assumptions
The
circumcenter
of a triangle is the center of a circle which passes through all three vertices of a triangle.
The
orthocenter
of a triangle is the intersection of the 3 altitudes (perpendicular from vertices to opposite side).
You may choose to read this page on extended sine rule .
The answer is 85.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Let D be the point on the circumcircle so that B D is a diameter. It's easy to see A H C D is a parallelogram. So D C = A H = A O = R . Hence D C = 2 1 B D . Therefore ∠ B A C = ∠ B D C = 6 0 ∘ . So ∠ A B C = 8 5 ∘ .
Let ∠ O A C and ∠ O A B be α and β respectively. Then ∠ B A C = α + β , ∠ A B C = 9 0 ∘ − α . [Do you see why? It's just angle chasing. - Calvin]
Let A C = 1 . Then A O = 2 ⋅ cos α 1 , A H = sin ( 9 0 ∘ − α ) cos ( α + β ) = cos α cos ( α + β ) . Hence, cos ( α + β ) = 2 1 , so ∠ B A C = α + β = 6 0 ∘ [Since we are given that A B C is an acute triangle - Calvin].
If we choose the origin to be the orthocentre O , then the position vectors of A , B , C are a , b , c , where ∣ a ∣ = ∣ b ∣ = ∣ c ∣ = R , where R is the outradius.
It is a standard calculation that the position vector of the orthocentre is O H = a + b + c . Thus the condition of the question states that ∣ b + c ∣ = R , and so R 2 = 2 R 2 + b ⋅ c . Thus b ⋅ c = − 2 1 R 2 . The angle between b and c is 2 A , so we deduce that cos 2 A = − 2 1 . Thus 2 A = 1 2 0 ∘ , and hence A = 6 0 ∘ . Since C = 3 5 ∘ , it follows that B = 8 5 ∘ .
In this special case, let H be the same point as O, just to keep things simple. The altitudes of all the sides must be the same because the orthocenter is in the same spot of the circumcenter. And because of that, the 3 angles of the triangle must be all the same. Since a triangle has 180 degrees, you divide 180 by 3 and get 60 degrees.
Thats triangle make a same long.we can prove that with sin rule a / s i n a = b / s i b = c / s i n c = 2 R we get s i n a = s q r t ( 2 ) / 3 so <BAC is 60 degree
We draw O X ⊥ B C . We use the fact that A H = 2 O X ,i.e the distance of the orthocentre from vertex A is twice the distance of the the circumcenter from the side opposite to vertex A [ It has a proof, which i'm not going to give here]. Thus, in right angled triangle O X C , we have O X = 2 1 × A H = 2 1 × A O , O C = A O (since they are the circumradii). Morover, O is the centre of the circumcircle of △ A B C . Hence, we have ∠ B O C = 2 ∠ A And as △ O B X ≅ △ O X C (can be easily verifired) , we have ∠ X O C = ∠ A .
Now, cos ∠ X O C = O C O X = 2 1 . Hence ∠ X O C = ∠ A = 6 0 ∘ or 1 2 0 ∘ . But ∠ A is acute and we conclude ∠ A = 6 0 ∘ . Thus, ∠ B = 1 8 0 ∘ − 6 0 ∘ − 3 5 ∘ = 8 5 ∘

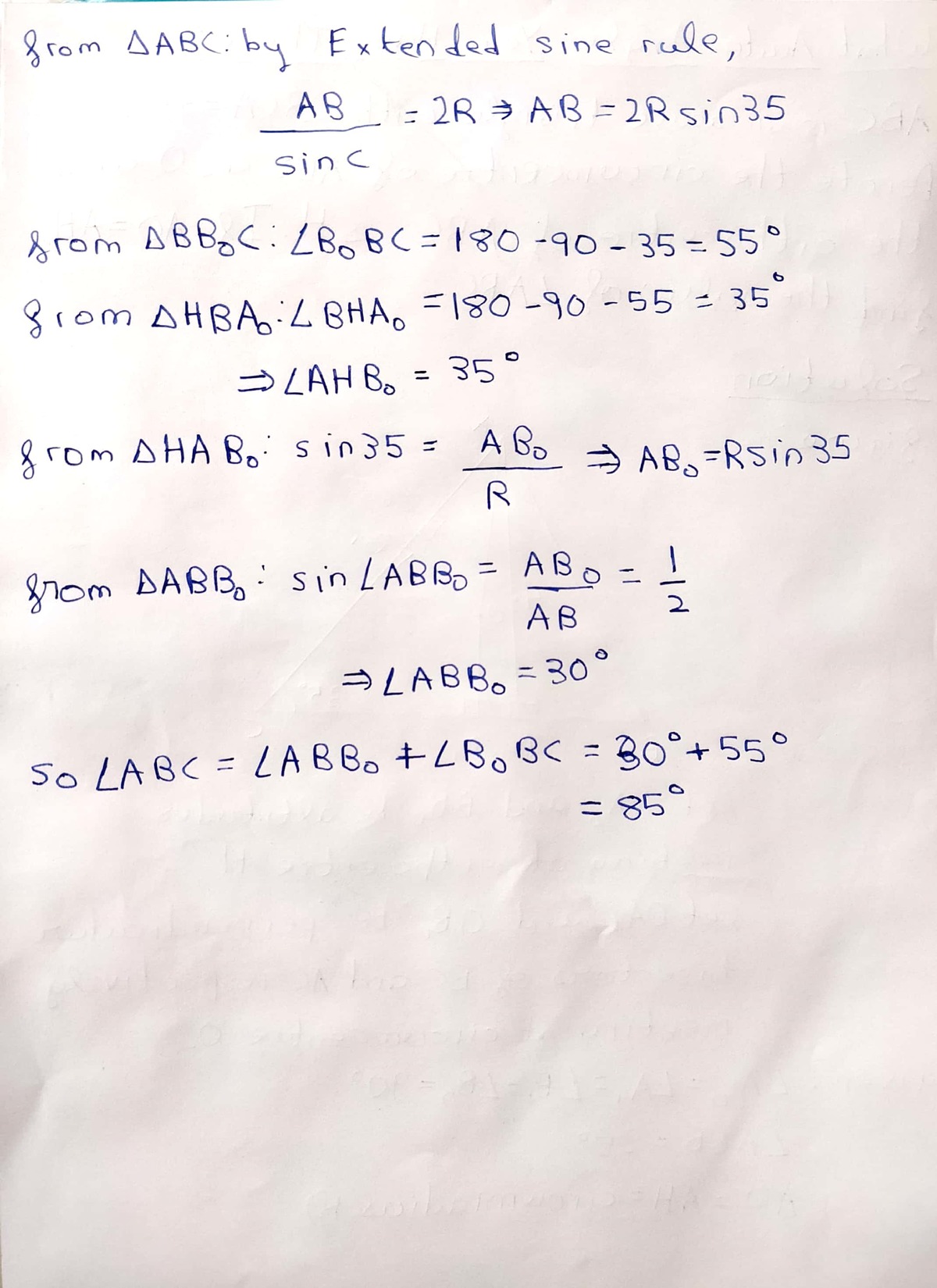
Let M be the midpoint of BC. It is well-known (and easy to prove with Euler line or homothety) that AH = 2OM. Thus BO = CO = AO = AH = 2OM. Because OM is perpendicular to BC <MOB = <MOC = arccos(1/2) = 60 degrees, so <BOC = 60 degrees. Then it follows that <BAC = 60 degrees.