What are the coordinates?
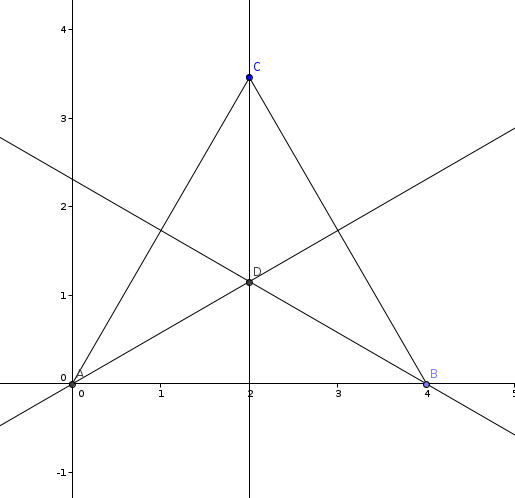
If is an equilateral triangle 4 units in length, where is it's incentre, what are the coordinates of ?
I assume you can see the value is 2, so find the value to two decimal places.
The answer is 1.15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since it is equilateral, we know CAB is 60 degrees. To find the incentre, we bisect that angle, giving us a 30 degree angle at CAD. We also know AC is 4 units long. We can realize easily that AD is congruent to CD by ASA, therefore ADC will be 120 degrees. We can solve for AD using the law of sines: 4 s i n ( 1 2 0 ) = A D s i n ( 3 0 ) A D = s i n ( 1 2 0 ) 4 ⋅ s i n ( 3 0 ) ≈ 2 . 3 1 We now have the polar coordinates: (2.31, 30) which we can convert into Cartesian coordinates: x = c o s ( 3 0 ) 2 . 3 1 = 2 y = s i n ( 3 0 ) 2 . 3 1 ≈ 1 . 1 5 4 7 . Rounding to nearest hundredths, 1 . 1 5 .