What Can We Equate?

Geometry Level 5

The lengths of three sides of $\triangle ABC$ are $AB=a+3b$ , $BC=a+2b$ , and $CA=a+b$ where $a$ is a positive integer and $0<b\leq 1$ . If the length of the altitude to side $BC$ is $a$ , find the number of triangles, no pair being similar, which satisfy the conditions.

The answer is 1.

1 solution

Grant Bulaong
Jun 12, 2016

We can equate the area of $\triangle ABC$ given by Heron's Formula and the Base & Altitude Formula.

$\sqrt{ \left(\frac{3}{2}a+3b\right) \left(\frac{a}{2}\right) \left(\frac{a}{2}+b\right) \left(\frac{a}{2}+2b\right)}=a\left(\frac{a}{2}+b\right)$

The equation gives us $12b=a$ , a fixed ratio. Since $0<b\leq1$ and $a$ is an integer, we have $a \in \{1,2,3,...,11,12\}$ . Hence our answer is $12$ .

Moderator note:

Note that all of these triangles are similar to each other. Hence there is only 1 solution.

I had done just the same thing.

ALEKHYA CHINA - 5 years ago

Same Way!! But had to use wolfram alpha to get a=12b; is there an easy way out?

Yatin Khanna - 5 years ago

You can factor out $\left(\frac{3}{2}a+3b\right)=(3)\left(\frac{1}{2}a+b\right)$ and you will have a factor which appears on both sides.

Grant Bulaong - 5 years ago

Got it!! Thanks!

Yatin Khanna - 5 years ago

Out of the box thought !! (+ 2)

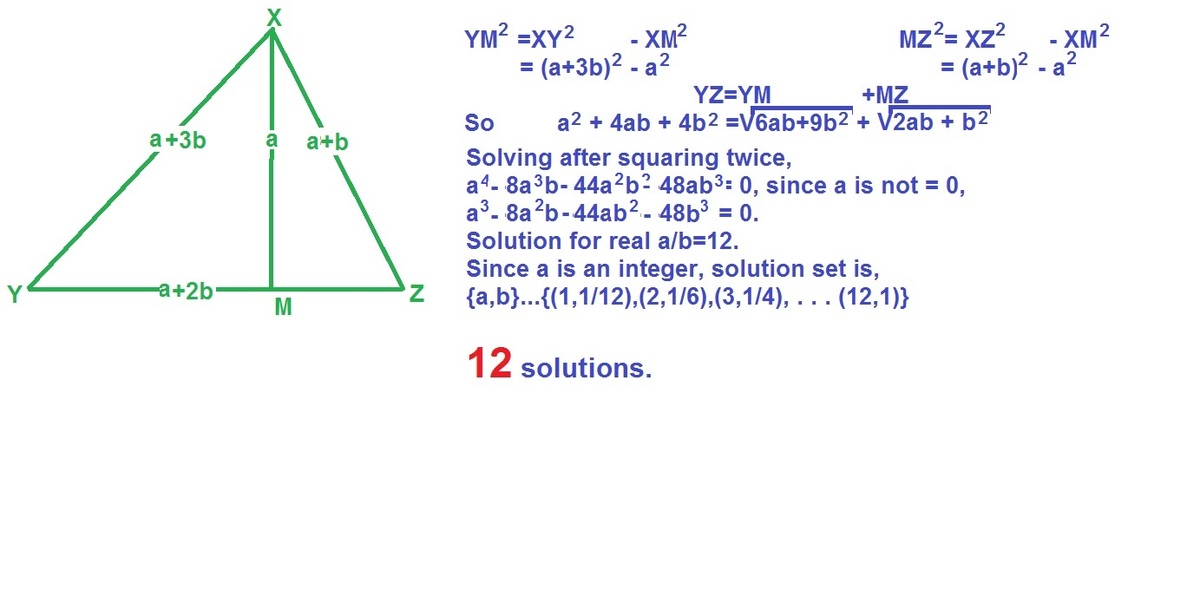
Aakash Khandelwal - 4 years, 12 months ago

Niranjan Khanderia - 4 years, 4 months ago

@Grant Bulaong The question says that no two pair of triangles can be similar , but all the 12 triangles are similar to each other. Hence , you should rather specify in the problem that no two triangles are congruent to each other.

Thanks!

Ankit Kumar Jain - 4 years, 2 months ago

What Can We Equate?

The answer is 1.

1 solution

Moderator note:

0 pending reports