What Center Is Most Crucial?

Geometry Level 4

A triangle P Q R PQR was drawn on a Cartesian plane such that there exists a point O O for which the distance P O ‾ = Q O ‾ = R O ‾ \overline {PO } = \overline{QO} = \overline{RO} is equal to 4. And two of the vertices of this triangle have coordinates ( 1 , 3 ) (1,3) and ( 5 , 6 ) (5,6) .

Given that the sine of one of the interior angles of this triangle must always be a constant. Find this constant.

Give your answer to 3 decimal places.


The answer is 0.625.

Pi Han Goh by Pi Han Goh , 30, Malaysia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

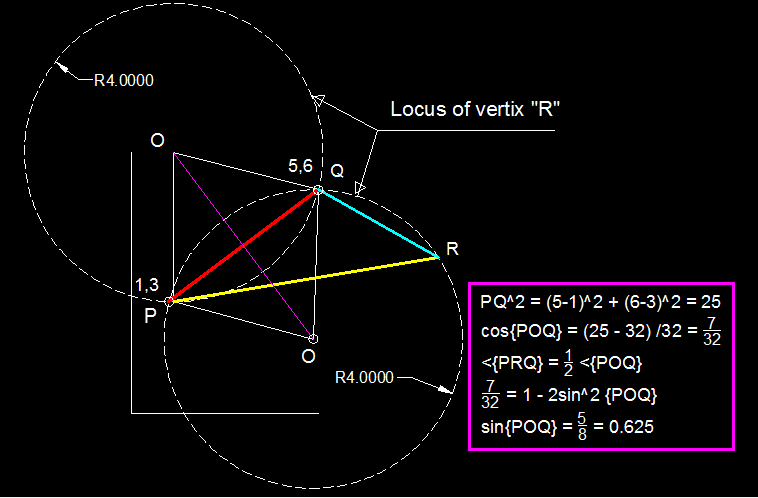
Point O O appears to be the circumcentre, and the triangle P Q R PQR has circumradius 4. Applying the sine rule, we find that p sin ⁡ P = 2 r ⇒ 5 sin ⁡ P = 8 ⇒ sin ⁡ P = 5 8 = 0.625 \frac{p}{\sin P}=2r\Rightarrow \frac{5}{\sin P}=8\Rightarrow \sin P=\frac{5}{8}=0.625

1 Helpful 0 Interesting 0 Brilliant 0 Confused
Ahmad Saad
Jun 19, 2016

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...