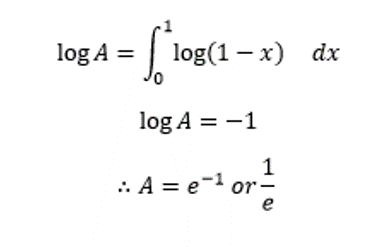What could this limit be?
n → ∞ lim ( n n n ! ) n 1 = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I'm going to use Stirling formula n → ∞ lim ( n n n ! ) n 1 = n → ∞ lim ⎝ ⎛ n 2 π n ( n 1 ) ( e n ) ⎠ ⎞ = e 1 due to n → ∞ lim 2 n 2 π n = 1
Did the aame
Log in to reply
Well done,haha! I almost always use Stirling's formula in limits when the factorial number is inside of it. Almost always, but not always..
Wow ,thanks for sharing a new technique ., i did not know this technique .
Log in to reply
thank you very much, this new formula formula for you is an old known formula for me, haha... it's not you,it's me, I'm getting older...
Also did it the same way!
using e p s i l o n - d e l t a definition :p
Let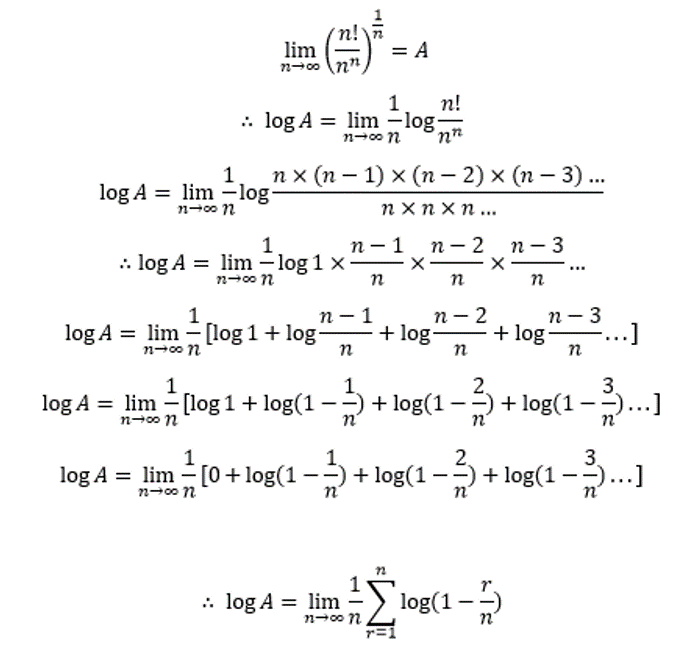 If one replaces
r
/
n
by
x
and
1
/
n
by
d
x
, the equation now becomes
If one replaces
r
/
n
by
x
and
1
/
n
by
d
x
, the equation now becomes